题目内容
“a>1”是“对任意的正数x,不等式2x+
≥1成立”的( )
| a |
| x |
分析:先求命题“对任意的正数x,不等式2x+
≥1成立”的充要条件,再利用集合法判断两命题间的充分必要关系
| a |
| x |
解答:解:对任意的正数x,不等式2x+
≥1成立?对任意的正数x,y=2x+
的最小值大于或等于1
∵x>0时,y=2x+
≥2
=2
∴2
≥1即 a≥
∴命题“对任意的正数x,不等式2x+
≥1成立”的充要条件为a≥
∵{a|a>1}?{a|a≥
}
∴“a>1”是“对任意的正数x,不等式2x+
≥1成立”的充分不必要条件
故选 B
| a |
| x |
| a |
| x |
∵x>0时,y=2x+
| a |
| x |
2x•
|
| 2a |
∴2
| 2a |
| 1 |
| 8 |
∴命题“对任意的正数x,不等式2x+
| a |
| x |
| 1 |
| 8 |
∵{a|a>1}?{a|a≥
| 1 |
| 8 |
∴“a>1”是“对任意的正数x,不等式2x+
| a |
| x |
故选 B
点评:本题考查了命题充要条件的判断方法,求命题充要条件的方法,不等式恒成立问题的解法,转化化归的思想方法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
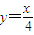 上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.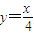 上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.