Question

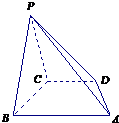在四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠ABC=90°，AB=PB=PC=BC=2CD，平面PBC⊥平面ABCD．
（Ⅰ）求证：AB⊥平面PBC；
（Ⅱ）求平面PAD和平面BCP所成二面角（小于90°）的大小；
（Ⅲ）在棱PB上是否存在点M使得CM∥平面PAD？若存在，求

PM

PB

的值；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）证明AB⊥平面PBC，利用面面垂直的性质，根据AB⊥BC，平面PBC⊥平面ABCD，即可得证；
（Ⅱ）取BC的中点O，连接PO，证明PO⊥平面ABCD，以O为原点，OB所在的直线为x轴，在平面ABCD内过O垂直于BC的直线为y轴，OP所在的直线为z轴建立空间直角坐标系O-xyz，求出平面PAD的法向量

m

=(1，-2，-

3

)，平面BCP的一个法向量

n

=(0，1，0)，利用向量的夹角公式，即可求得平面ADP和平面BCP所成的二面角；
（Ⅲ）在棱PB上存在点M使得CM∥平面PAD，此时

PM

PB

=

1

2

，证明平面MNC∥平面PAD，可得∥平面PAD．

解答：（Ⅰ）证明：因为∠ABC=90°，所以AB⊥BC．…（1分）
因为平面PBC⊥平面ABCD，平面PBC∩平面ABCD=BC，AB?平面ABCD，
所以AB⊥平面PBC；…（3分）
（Ⅱ）解：取BC的中点O，连接PO．
因为PB=PC，所以PO⊥BC．
因为平面PBC⊥平面ABCD，平面PBC∩平面ABCD=BC，PO?平面PBC，
所以PO⊥平面ABCD．…（4分）
如图，以O为原点，OB所在的直线为x轴，在平面ABCD内过O垂直于BC的直线为y轴，OP所在的直线为z轴建立空间直角坐标系O-xyz．
不妨设BC=2．由直角梯形ABCD中AB=PB=PC=BC=2CD可得P（0，0，

3

），D（-1，1，0），A（1，2，0）．
所以

DP

=(1，-1，

3

)，

DA

=(2，1，0)．
设平面PAD的法向量

m

=(x，y，z)．
因为

m • DP =0 m • DA =0

，所以 

x-y+ 3 z=0 2x+y=0

令x=1，则y=-2，z=-

3

．
所以

m

=(1，-2，-

3

)．…（7分）
取平面BCP的一个法向量

n

=(0，1，0)，所以cos＜

m

，

n

＞=-

2

2

．
所以平面ADP和平面BCP所成的二面角（小于90°）的大小为

π

4

．…（9分）
（Ⅲ）解：在棱PB上存在点M使得CM∥平面PAD，此时

PM

PB

=

1

2

．理由如下：…（10分）
取AB的中点N，连接CM，CN，MN，则MN∥PA，AN=

1

2

AB．
因为AB=2CD，所以AN=CD．
因为AB∥CD，所以四边形ANCD是平行四边形．
所以CN∥AD．
因为MN∩CN=N，PA∩AD=A，
所以平面MNC∥平面PAD（13分）
因为CM?平面MNC，所以CM∥平面PAD．…（14分）

点评：本题考查线面垂直、线面平行，考查面面角，解题的关键是掌握线面垂直、线面平行的判定方法，利用空间向量求解面面角．