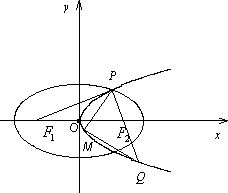题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
证明:当直线AB的斜率不存在时,设直线AB的方程为: 则
|
(2) |
由已知 设
故 =
∴a、b、c成等差数列……………………………………………………8分 |
(3) |
解法一:
由(Ⅱ)可知 ①若AB⊥x轴,则
②若
同理可得
即 易知∠PFO,∠BPF,∠APF都是锐角
③若 总上所述, 解法二:
①如图,若AB⊥x轴,则
②若
设AB中点为M,则 = 所以PM是梯形ABDC的中位线,故P是CD中点
③若 ∴ |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目