题目内容
已知点M(-5,0),F(1,0),点K满足 =2
=2 ,P是平面内一动点,且满足|
,P是平面内一动点,且满足| |•|
|•| |=
|= •
• .
.(1)求P点的轨迹C的方程;
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与曲线C相交于点A,B,l2与曲线C相交于点D,E,求四边形ADBE的面积的最小值.
【答案】分析:(1)先确定K的坐标,再利用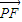 |•|
|•| |=
|=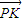 •
•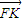 ,即可求P点的轨迹C的方程;
,即可求P点的轨迹C的方程;
(2)设出直线方程,与抛物线方程联立,求得|AB|,|DE|,表示出面积,利用基本不等式,即可求得最值.
解答:解:(1)设K(x,y),P(x,y)
∵M(-5,0),F(1,0),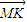 =2
=2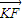 ,
,
∴(x+5,y)=2(1-x,-y)
∴x=-1,y=0,∴K(-1,0)
∵|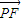 |•|
|•|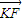 |=
|=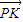 •
•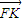 ,
,
∴2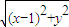 =(-1-x,-y)•(-2,0)
=(-1-x,-y)•(-2,0)
∴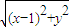 =1+x,即y2=4x;
=1+x,即y2=4x;
(2)设l1的方程为x=ny+1(n≠0),与y2=4x联立,消去x可得y2-4ny-4=0
设A(x1,y1),B(x2,y2),则y1+y2=4n,y1y2=-4
∴|AB|=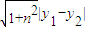 =4(n2+1)
=4(n2+1)
∵l1⊥l2,∴l2的方程为x=-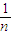 y+1,与y2=4x联立,
y+1,与y2=4x联立,
同理可得|DE|=4(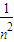 +1)
+1)
∴四边形ADBE的面积为 |AB||DE|=8(n2+1)(
|AB||DE|=8(n2+1)( +1)=8(n2+
+1)=8(n2+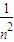 +2)≥32
+2)≥32
当且仅当n2=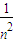 ,即n=±1时,四边形ADBE的面积的最小值为32.
,即n=±1时,四边形ADBE的面积的最小值为32.
点评:本题考查轨迹方程,考查向量知识的运用,考查直线与抛物线的位置关系,考查四边形面积的计算,考查基本不等式,属于中档题.
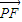 |•|
|•| |=
|=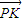 •
•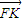 ,即可求P点的轨迹C的方程;
,即可求P点的轨迹C的方程;(2)设出直线方程,与抛物线方程联立,求得|AB|,|DE|,表示出面积,利用基本不等式,即可求得最值.
解答:解:(1)设K(x,y),P(x,y)
∵M(-5,0),F(1,0),
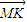 =2
=2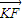 ,
,∴(x+5,y)=2(1-x,-y)
∴x=-1,y=0,∴K(-1,0)
∵|
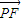 |•|
|•|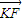 |=
|=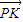 •
•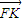 ,
,∴2
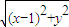 =(-1-x,-y)•(-2,0)
=(-1-x,-y)•(-2,0)∴
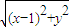 =1+x,即y2=4x;
=1+x,即y2=4x;(2)设l1的方程为x=ny+1(n≠0),与y2=4x联立,消去x可得y2-4ny-4=0
设A(x1,y1),B(x2,y2),则y1+y2=4n,y1y2=-4
∴|AB|=
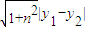 =4(n2+1)
=4(n2+1)∵l1⊥l2,∴l2的方程为x=-
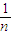 y+1,与y2=4x联立,
y+1,与y2=4x联立,同理可得|DE|=4(
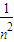 +1)
+1)∴四边形ADBE的面积为
 |AB||DE|=8(n2+1)(
|AB||DE|=8(n2+1)( +1)=8(n2+
+1)=8(n2+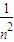 +2)≥32
+2)≥32当且仅当n2=
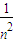 ,即n=±1时,四边形ADBE的面积的最小值为32.
,即n=±1时,四边形ADBE的面积的最小值为32.点评:本题考查轨迹方程,考查向量知识的运用,考查直线与抛物线的位置关系,考查四边形面积的计算,考查基本不等式,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 所成的比为2.P是平面上一动点,且满足
所成的比为2.P是平面上一动点,且满足 .
.