题目内容
19.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),有以下结论:①求f(2012)=0;
②函数f(x)的图象关于直线x=2对称;
③若f(x)在[-2,0]上单调递增,则f(x)在[-2,2]上单调递增;
④若f(x)满足在区间[0,2]上是增函数的条件,且f(2)=1,则在x∈R上有f(x)∈[-1,1].
其中正确的结论是①③④.
分析 对四个选项分别进行判断,即可得出结论.
解答 解:(1)∵f(x-4)=-f(x),∴f(x-8)=-f(x-4)=f(x),∴函数的周期为8,
∴f(2012)=f(8×251+4)=f(4)=-f(0)=0,正确;
②定义在R上的奇函数f(x)满足f(x-4)=-f(x),则f(x-4)=f(-x),∴f(x-2)=f(-x-2),∴函数f(x)关于直线x=-2对称,不正确;
③若f(x)在[-2,0]上单调递增,函数f(x)是奇函数,则f(x)在[-2,2]上单调递增,正确;
④若f(x)满足在区间[0,2]上是增函数的条件,且f(2)=1,则在x∈[-2,2]上有f(x)∈[-1,1],∵函数的周期为8,∴在x∈R上有f(x)∈[-1,1],正确.
故答案为:①③④.
点评 本题考查函数的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
7.如图,四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$,则必有( )
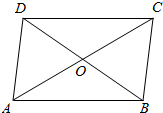

| A. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ | B. | $\overrightarrow{OA}$=$\overrightarrow{OC}$ | C. | $\overrightarrow{AC}$=$\overrightarrow{DB}$ | D. | $\overrightarrow{DO}$=$\overrightarrow{OB}$ |
4.函数f(x)=x3+3x2+3ax-4既有极大值又有极小值,则函数g(x)=x+$\frac{a}{x}$-2a在区间(1,+∞)上一定( )
| A. | 有最小值 | B. | 有最大值 | C. | 是减函数 | D. | 是增函数 |
8.已知$sin(a+\frac{π}{6})-cosa=\frac{1}{3},则cos(2a-\frac{π}{3})$=( )
| A. | -$\frac{5}{18}$ | B. | $\frac{5}{18}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |