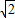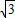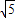题目内容
已知a>b>c,且直线ax+cy=2平分圆(x-1)2+(y+1)2=1,当实数λ≤ +
+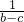 恒成立时,λ的最大值为________.
恒成立时,λ的最大值为________.
2
分析:根据题意,求出圆的圆心坐标,又由直线始终平分圆,则直线过圆心,将圆心坐标代入直线方程,可得a-c=2,由基本不等式求出 +
+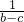 的最小值,又实数λ≤
的最小值,又实数λ≤ +
+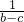 恒成立时,λ≤
恒成立时,λ≤ +
+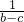 的最小值,分析可得λ的最大值,即可得答案.
的最小值,分析可得λ的最大值,即可得答案.
解答:根据题意,圆:(x-1)2+(y+1)2=1,则其圆心坐标为(1,-1),
又由直线ax+cy=2平分圆(x-1)2+(y+1)2=1,
则直线过圆心,所以有a×1-c×1=2,变形可得a-c=2;
则有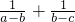 =(a-b)+(b-c)+
=(a-b)+(b-c)+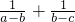 -2≥2,
-2≥2,
(当且仅当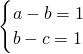 时等号成立)
时等号成立)
∴当实数λ≤ +
+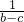 恒成立时,λ≤2,
恒成立时,λ≤2,
∴λ的最大值为 2.
故答案为:2
点评:本题考查直线与圆的位置关系以及基本不等式的运用,难点是利用不等式的关系,关键是分析得到直线ax+cy=2过圆的圆心.
分析:根据题意,求出圆的圆心坐标,又由直线始终平分圆,则直线过圆心,将圆心坐标代入直线方程,可得a-c=2,由基本不等式求出
 +
+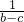 的最小值,又实数λ≤
的最小值,又实数λ≤ +
+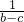 恒成立时,λ≤
恒成立时,λ≤ +
+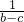 的最小值,分析可得λ的最大值,即可得答案.
的最小值,分析可得λ的最大值,即可得答案.解答:根据题意,圆:(x-1)2+(y+1)2=1,则其圆心坐标为(1,-1),
又由直线ax+cy=2平分圆(x-1)2+(y+1)2=1,
则直线过圆心,所以有a×1-c×1=2,变形可得a-c=2;
则有
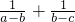 =(a-b)+(b-c)+
=(a-b)+(b-c)+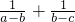 -2≥2,
-2≥2,(当且仅当
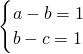 时等号成立)
时等号成立)∴当实数λ≤
 +
+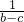 恒成立时,λ≤2,
恒成立时,λ≤2,∴λ的最大值为 2.
故答案为:2
点评:本题考查直线与圆的位置关系以及基本不等式的运用,难点是利用不等式的关系,关键是分析得到直线ax+cy=2过圆的圆心.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆
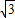 ,若球O的体积为
,若球O的体积为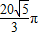 ,则这个直三棱柱的体积等于( )
,则这个直三棱柱的体积等于( )