题目内容
已知A、B、C、D四点坐标分别为A(1,0)、B(4,3)、C(2,4)、D(0,2)，试证明四边形ABCD是梯形.
证明:∵
=(4,3)-(1,0)=(3,3),
=(0,2)-(2,4)=(-2,-2),
∴
=-
.
故
与
共线，
即
∥
.
∴AB∥CD.
∵
=(0,2)-(1,0)=(-1,2),
=(2,4)-(4,3)=(-2,1),
又∵(-1)×1-2×(-2)≠0,
∴AD不平行于BC.
∴四边形ABCD是梯形.
练习册系列答案
相关题目
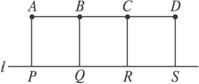
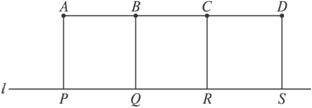
如图，A、B、C、D是某煤矿的四个采煤点，l是公路，图中所标线段为道路，ABQP、BCRQ、CDSR近似于正方形．已知A、B、C、D四个采煤点每天的采煤量之比约为5：1：2：3，运煤的费用与运煤的路程、所运煤的重量都成正比．现要从P、Q、R、S中选出一处设立一个运煤中转站，使四个采煤点的煤运到中转站的费用最少，则地点应选在（ ）
