题目内容
在四棱锥P-ABCD中,底面ABCD是正方形,PD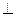 底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
(1)求证:MN∥平面PCD
(2)求证:平面PAC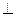 平面PBD
平面PBD
(3)求MN与底面ABCD所成角的大小
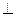 底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)(1)求证:MN∥平面PCD
(2)求证:平面PAC
 平面PBD
平面PBD(3)求MN与底面ABCD所成角的大小

(1)设Q是PD中点,连结MQ,CQ.有MQ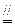 CN,得MNCQ是平行四边形
CN,得MNCQ是平行四边形
 MN∥CQ,又CQ
MN∥CQ,又CQ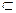 平面PCD,MN
平面PCD,MN 平面PCD
平面PCD
 MN∥平面PCD
MN∥平面PCD
(2) 平面ABCD,
平面ABCD, 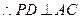
又底面ABCD是正方形,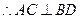
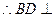 平面PAC
平面PAC
又BD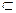 平面PBD
平面PBD 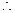 平面PAC
平面PAC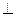 平面PBD
平面PBD
(3)设G是AD中点,连结MG,NG, 则有MG∥PD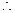 MG
MG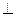 平面ABCD
平面ABCD
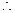 ∠MNG就是MN与平面ABCD所成的角
∠MNG就是MN与平面ABCD所成的角
由PD=AD=1得MG=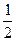 , NG=1,
, NG=1,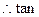 ∠MNG=
∠MNG=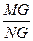 =
=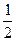
即MN与平面ABCD所成角的正切值为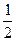
 CN,得MNCQ是平行四边形
CN,得MNCQ是平行四边形 MN∥CQ,又CQ
MN∥CQ,又CQ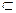 平面PCD,MN
平面PCD,MN 平面PCD
平面PCD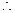 MN∥平面PCD
MN∥平面PCD(2)
 平面ABCD,
平面ABCD, 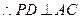
又底面ABCD是正方形,
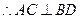
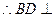 平面PAC
平面PAC 又BD
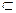 平面PBD
平面PBD 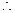 平面PAC
平面PAC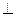 平面PBD
平面PBD(3)设G是AD中点,连结MG,NG, 则有MG∥PD
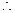 MG
MG 平面ABCD
平面ABCD ∠MNG就是MN与平面ABCD所成的角
∠MNG就是MN与平面ABCD所成的角由PD=AD=1得MG=
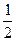 , NG=1,
, NG=1,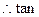 ∠MNG=
∠MNG=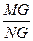 =
=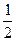
即MN与平面ABCD所成角的正切值为
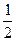
略

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 为两条异面直线,
为两条异面直线, 为其公垂线,直线
为其公垂线,直线 ,则
,则 与
与 ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
 中,
中, ,又
,又 ⊥平面
⊥平面 .
. 上存在一点
上存在一点 ,使
,使 ,
,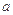 的取值范围;
的取值范围; 的余弦值.
的余弦值.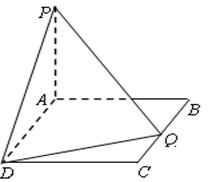

 ,侧面积为
,侧面积为
 ,则此圆锥的体积为__________
,则此圆锥的体积为__________
 的正方体
的正方体 中,异面直线
中,异面直线 与
与 所成的角等于( )
所成的角等于( )


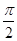

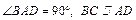 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.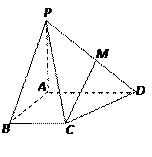
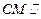 平面PAB;
平面PAB; 中,底面
中,底面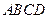 为直角梯形,
为直角梯形,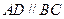 ,
,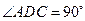 ,平面
,平面 ⊥底面
⊥底面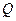 为AD的中点,
为AD的中点,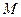 是棱
是棱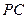 上的点,
上的点,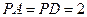 ,
,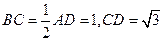 .(1)若
.(1)若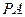
 ;(2)求证:平面
;(2)求证:平面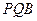 ⊥平面
⊥平面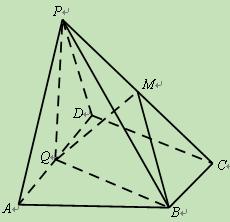
 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积