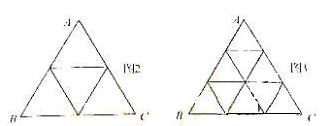
题目内容
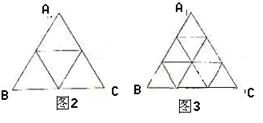
将正△ABC分割成n2(n≥2,n∈N)个全等的小正三 角形(图1,图2分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=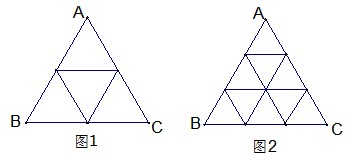
分析:根据等差中项法分别求解n=2,3,4时的值,由此归纳出f(n)的值即可.
解答:解:由题意可得,(各点放的数用该点的坐标表示)
当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1
2(D+E+F)=2(A+B+C)=2,D+E+F=1
∴f(2)=2=
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1
从而可得D+E+H+I+F+F=2(A+B+C)=2
同样根据等差中项可得,M的数为
∴f(3)=3+
=
=
同理可得,f(4)=5=
f(n)=
故答案为:
,


当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1
2(D+E+F)=2(A+B+C)=2,D+E+F=1
∴f(2)=2=
| 3×4 |
| 6 |
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1
从而可得D+E+H+I+F+F=2(A+B+C)=2
同样根据等差中项可得,M的数为
| 1 |
| 3 |
∴f(3)=3+
| 1 |
| 3 |
| 10 |
| 3 |
| 4×5 |
| 6 |
同理可得,f(4)=5=
| 5×6 |
| 6 |
f(n)=
| (n+1)(n+2) |
| 6 |
故答案为:
| 10 |
| 3 |
| (n+1)(n+2) |
| 6 |


点评:本题目主要考查了数列的通项公式的求解在实际问题中的应用,解题的关键是灵活利用等差中项,进行求解.考查了考试发现问题、解决问题的能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目