题目内容
已知cosα= ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α< ,
,(Ⅰ)求tan2α的值;
(Ⅱ)求β.
【答案】分析:(1)欲求tan2α的值,由二倍角公式知,只须求tanα,欲求tanα,由同角公式知,只须求出sinα即可,故先由题中coaα的求出sinα 即可;
(2)欲求角,可通过求其三角函数值结合角的范围得到,这里将角β配成β=α-(α-β),利用三角函数的差角公式求解.
解答:解:(Ⅰ)由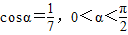 ,得
,得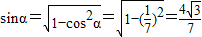
∴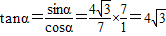 ,于是
,于是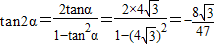
(Ⅱ)由0<β<α<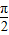 ,得
,得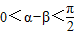 ,
,
又∵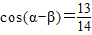 ,∴
,∴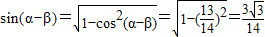
由β=α-(α-β)得:cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=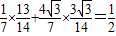
所以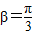 .
.
点评:本题考查三角恒等变形的主要基本公式、三角函数值的符号,已知三角函数值求角以及计算能力.
(2)欲求角,可通过求其三角函数值结合角的范围得到,这里将角β配成β=α-(α-β),利用三角函数的差角公式求解.
解答:解:(Ⅰ)由
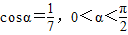 ,得
,得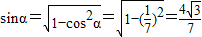
∴
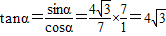 ,于是
,于是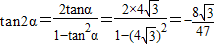
(Ⅱ)由0<β<α<
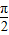 ,得
,得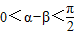 ,
,又∵
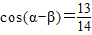 ,∴
,∴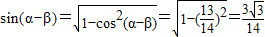
由β=α-(α-β)得:cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=
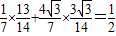
所以
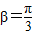 .
.点评:本题考查三角恒等变形的主要基本公式、三角函数值的符号,已知三角函数值求角以及计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 (2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,
(2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,