题目内容
 在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,E、F分别为BC、PD的中点,PA=AB.
在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,E、F分别为BC、PD的中点,PA=AB.(1)求证:EF∥平面PAB;
(2)求直线EF与平面PCD所成的角.
分析:(1)法一:利用线面平行的判定定理证明:取PA中点K,连KF、KB则根据三角形中位线定理和正方形ABCD的性质可达得四边形KBEF为平行四边形即KB∥EF然后根据线面平行的判定定理即可得证.
法二:利用空间向量的基本定理证明:根据向量减法的三角形法则可得
=
-
而根据向量加法的平行四边形法则可得
=
(
+
),
=
+
再结合
=
可得
=
-
即可得证.
法三:利用面面平行可证线面平行:取AD中点为M连接EM,FM根据面面平行的判定定理可证面PAB∥面EFM即可得出EF∥平面PAB
(2)法一:可采用补形法即四棱锥还原成正方体PRST-ABCD(如图)去DT的中点L连接CL则可得四边形ECLF为平行四边形即EF∥CL所以直线EF与平面PCD所成的角即为直线CL与
平面PCD所成的角而根据正方体的性质易得平面PADT⊥平面PRCD 则根据面面垂直的性质定理可知L在平面PRCD上的射影M必在PD上则∠MCL即为直线EF与平面PCD所成的角然后在三角形LMC中求出∠MCL即可.
法二:空间向量法:建立空间直角坐标系设PA=AB=BC=1求出面PCD的法向量
和
然后根据向量的夹角公式可求出cos<
,
>=
的值然后根据cos<
,
>的正负即可得解(若cos<
,
>>0则所求角为
-<
,
>,若cos<
,
><0则所求角为<
,
>-
).
法三:余角法:连接AF,AE根据线面垂直的判定定理可证出AF⊥面PCD故EF与面PCD的夹角即为∠AFE的余角然后利用余弦定理求出cos∠AFE即可得解.
法二:利用空间向量的基本定理证明:根据向量减法的三角形法则可得
| EF |
| AF |
| AE |
. |
| AF |
| 1 |
| 2 |
. |
| AD |
. |
| AP |
. |
| AE |
. |
| AB |
. |
| BE |
. |
| BE |
| 1 |
| 2 |
. |
| AD |
. |
| EF |
| 1 |
| 2 |
. |
| AP |
. |
| AB |
法三:利用面面平行可证线面平行:取AD中点为M连接EM,FM根据面面平行的判定定理可证面PAB∥面EFM即可得出EF∥平面PAB
(2)法一:可采用补形法即四棱锥还原成正方体PRST-ABCD(如图)去DT的中点L连接CL则可得四边形ECLF为平行四边形即EF∥CL所以直线EF与平面PCD所成的角即为直线CL与
平面PCD所成的角而根据正方体的性质易得平面PADT⊥平面PRCD 则根据面面垂直的性质定理可知L在平面PRCD上的射影M必在PD上则∠MCL即为直线EF与平面PCD所成的角然后在三角形LMC中求出∠MCL即可.
法二:空间向量法:建立空间直角坐标系设PA=AB=BC=1求出面PCD的法向量
| n |
| EF |
. |
| n |
. |
| EF |
| ||||
|
|
. |
| n |
. |
| EF |
. |
| n |
. |
| EF |
| π |
| 2 |
. |
| n |
. |
| EF |
. |
| n |
. |
| EF |
. |
| n |
. |
| EF |
| π |
| 2 |
法三:余角法:连接AF,AE根据线面垂直的判定定理可证出AF⊥面PCD故EF与面PCD的夹角即为∠AFE的余角然后利用余弦定理求出cos∠AFE即可得解.
解答: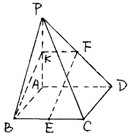 证明:(1)法一:取PA中点K,连KF、KB,由中位线定理知KF
证明:(1)法一:取PA中点K,连KF、KB,由中位线定理知KF
AD=BE.
∴四边形KBEF为平行四边形
∴KB∥EF(2分)
而KB?平面PAB,EF?平面PAB,
∴EF∥平面PAB(2分)
法二:证明:Θ
=
-
=
(
+
)-(
+
)
═
+
-
-
-
(2分)
=
+
-
-
=
-
∴EF∥平面PAB (2分)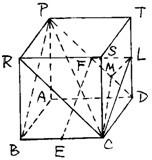
法三:取AD中点为M,则MF∥AP,ME∥AB,(2分)
又EM∩MF=M,BA∩PA=A,∴面PAB∥面EFM
又EF?面EMF,∴EF∥面PAB (2分)
(2)法一:将四棱锥还原成正方体PRST-ABCD(如图) (2分)
将线段EF按
平移成CL,于是只需考虑求直线CL与平面PRCD的夹角.
ΘCD⊥平面PADT
CD?平面PRCD,
∴平面PADT⊥平面PRCD (2分)
设L在平面PRCD上的射影为M,则M∈PD
∴ML=
,CL=
=
a(设正方体棱长为2a) (2分)
∴∠MCL=arcsin
=arcsin
即直线EF与平面PCD的夹角为arcsin
.(2分)
法二:如图所示建立空间直角坐标系,设PA=AB=BC=1
则P(0,0,1),D(0,1,0),B(1,0,0),
C(1,1,0),A(0,0,0)
∴E(1,
,0),F(0,
,
)
∴
=(-1,0,
),
=(0,1,-1),
=(-1,0,0)(2分)
设面PCD的法向量
=(0,x0,y0),则(0,x0,y0),
(0,1,-1)=0,(0,x0,y0),(-1,0,0)=0,x0=y0,故可令x0=y0=1.?
=(0,1,1)(2分)
∴该法向量与
的夹角为θ满足
cosθ=
=
(3分)
∴EF与平面PCD的夹角为
-arccos
=arcsin
(1分)
法三:设PA=AB=AD=2,连接AE,AF
ΘPA⊥面ABCD,CD?面ABCD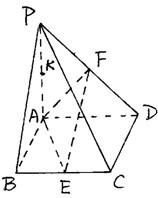
∴PA⊥CD …(1分)
而AD⊥CD,AD与PD交于D,
∴CD⊥面PAD,…(1分)
又AF?面PAD,
∴CD⊥AF …(1分)
又Θ△PAD为等腰Rt△,所以AF⊥PD
ΘPD与CD交于D,
∴AF⊥面PCD,…(1分)
∴EF与面PCD的夹角即为∠AFE的余角.
AF=
=
,AE=
=
,
EF=BK=
=
,
∴由余弦定理得cos∠AFE=
=
=
(3分)
∴EF与面PCD的夹角为
-arccos
=arcsin
(1分)
 证明:(1)法一:取PA中点K,连KF、KB,由中位线定理知KF
证明:(1)法一:取PA中点K,连KF、KB,由中位线定理知KF
| ||
. |
| 1 |
| 2 |
∴四边形KBEF为平行四边形
∴KB∥EF(2分)
而KB?平面PAB,EF?平面PAB,
∴EF∥平面PAB(2分)
法二:证明:Θ
| EF |
| AF |
| AE |
=
| 1 |
| 2 |
| AD |
| AP |
| AB |
| BE |
═
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AP |
| AB |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| BC |
=
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AP |
| AB |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AP |
| AB |
∴EF∥平面PAB (2分)

法三:取AD中点为M,则MF∥AP,ME∥AB,(2分)
又EM∩MF=M,BA∩PA=A,∴面PAB∥面EFM
又EF?面EMF,∴EF∥面PAB (2分)
(2)法一:将四棱锥还原成正方体PRST-ABCD(如图) (2分)
将线段EF按
| EC |
ΘCD⊥平面PADT
CD?平面PRCD,
∴平面PADT⊥平面PRCD (2分)
设L在平面PRCD上的射影为M,则M∈PD
∴ML=
| a | ||
|
| (2a)2+a2 |
| 5 |
∴∠MCL=arcsin
| ML |
| CL |
| ||
| 10 |
即直线EF与平面PCD的夹角为arcsin
| ||
| 10 |
法二:如图所示建立空间直角坐标系,设PA=AB=BC=1
则P(0,0,1),D(0,1,0),B(1,0,0),
C(1,1,0),A(0,0,0)
∴E(1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EF |
| 1 |
| 2 |
| FD |
| CD |
设面PCD的法向量
| n |
(0,1,-1)=0,(0,x0,y0),(-1,0,0)=0,x0=y0,故可令x0=y0=1.?
| n |
∴该法向量与
| EF |
cosθ=
(-1,0,
| ||||||
|
| ||
| 10 |
∴EF与平面PCD的夹角为
| π |
| 2 |
| ||
| 10 |
| ||
| 10 |
法三:设PA=AB=AD=2,连接AE,AF
ΘPA⊥面ABCD,CD?面ABCD

∴PA⊥CD …(1分)
而AD⊥CD,AD与PD交于D,
∴CD⊥面PAD,…(1分)
又AF?面PAD,
∴CD⊥AF …(1分)
又Θ△PAD为等腰Rt△,所以AF⊥PD
ΘPD与CD交于D,
∴AF⊥面PCD,…(1分)
∴EF与面PCD的夹角即为∠AFE的余角.
AF=
| PA | ||
|
| 2 |
| 22+1 |
| 5 |
EF=BK=
| 22+1 |
| 5 |
∴由余弦定理得cos∠AFE=
| AF2+EF2- AE2 |
| 2•AF•AE |
=
| 2 | ||
2
|
| ||
| 10 |
∴EF与面PCD的夹角为
| π |
| 2 |
| ||
| 10 |
| ||
| 10 |
点评:本题主要考察了线面平行的判定和线面角的求解,属较难题型.解题的关键是再证线面平行时常用到的方法有:线面平行的判定定理,空间向量的基本定理,面面平行可证线面平行而在求解线面角时补形法,空间向量法,余角法也是常用的方法需要说明的是其中余角法与空间向量法是如出一辙的!

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,