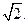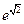题目内容
数列{an}的前n项和为Sn,且Sn= (an-1).
(an-1).
(1)求a1,a2;
(2)证明:数列{an}是等比数列;
(3)求an及Sn.
 (an-1).
(an-1).(1)求a1,a2;
(2)证明:数列{an}是等比数列;
(3)求an及Sn.
(1)a1=-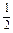 ,a2=
,a2=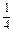 (2)证明见解析,(3)an=-(-
(2)证明见解析,(3)an=-(-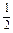 )n,Sn=
)n,Sn=
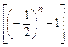
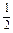 ,a2=
,a2=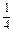 (2)证明见解析,(3)an=-(-
(2)证明见解析,(3)an=-(-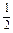 )n,Sn=
)n,Sn=
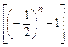
(1)解 ∵a1=S1= (a1-1),∴a1=-
(a1-1),∴a1=-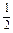 .
.
又a1+a2=S2= (a2-1),∴a2=
(a2-1),∴a2=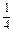 .
.
(2)证明 ∵Sn= (an-1),
(an-1),
∴Sn+1= (an+1-1),两式相减,
(an+1-1),两式相减,
得an+1= an+1-
an+1- an,即an+1=-
an,即an+1=-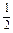 an,
an,
∴数列{an}是首项为-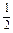 ,公比为-
,公比为-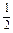 的等比数列.
的等比数列.
(3)解 由(2)得an=-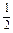 ·(-
·(-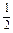 )n-1=-(-
)n-1=-(-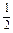 )n,Sn=
)n,Sn=
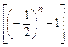 .
.
 (a1-1),∴a1=-
(a1-1),∴a1=-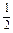 .
.又a1+a2=S2=
 (a2-1),∴a2=
(a2-1),∴a2=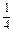 .
.(2)证明 ∵Sn=
 (an-1),
(an-1),∴Sn+1=
 (an+1-1),两式相减,
(an+1-1),两式相减,得an+1=
 an+1-
an+1- an,即an+1=-
an,即an+1=-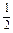 an,
an,∴数列{an}是首项为-
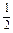 ,公比为-
,公比为-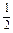 的等比数列.
的等比数列.(3)解 由(2)得an=-
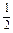 ·(-
·(-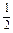 )n-1=-(-
)n-1=-(-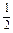 )n,Sn=
)n,Sn=
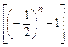 .
.
练习册系列答案
相关题目
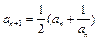 ,{bn}中
,{bn}中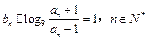 .
.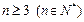 时,证明:
时,证明: .
.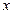 的多项式
的多项式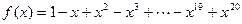 表为关于
表为关于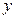 的多项式
的多项式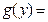
 其中
其中 则
则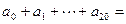 .
.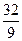 ;
;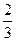 am-1,
am-1,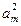 ,am+1+
,am+1+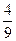 依次成等差数列.
依次成等差数列.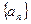 和
和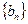 满足:
满足: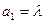 ,
,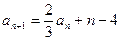 ,
,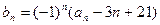 ,
,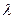 为实数,
为实数,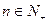 .
.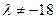 ,数列
,数列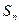 为数列
为数列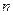 项和,是否存在实数
项和,是否存在实数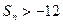 ?
?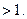 y
y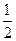 bx.
bx.