题目内容
【题目】某公司生产一种产品每年需投入固定成本为3万元，此外每生产1百件这种产品还需要增加投入1万元（总成本
固定成本
生产成本）．已知销售收入满足函数：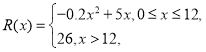
其中
（百件）为年产量，假定该产品产销平衡（即生产的产品都能卖掉）．
（1）请把年利润
表示为当年生产量
的函数；（利润
销售收入
总成本）
（2）当年产量为多少百件时，公司所获利润最大？最大利润为多少？
【答案】（1）
；（2）
百件时，
万元.
【解析】
试题分析：（1）销售收入减去成本
得到利润，所以；（2）第一段是二次函数，最大值在对称轴
处取得，
；第二段是减函数，没有最大值，综上百件时，万元.
试题解析：
（1）年利润为：
（2）当
时，
；
当
时，
（万元）；
当
时，
为减函数，
，
∴百件时，（万元）．
答：当年产量为10百件时，公司所获利润最大，最大利润为17万元．
练习册系列答案
相关题目
