题目内容
14.已知椭圆$C:\frac{x^2}{3}+{y^2}=1$的弦AB过点(-1,0),则弦AB中点的轨迹方程是x2+x+3y2=0.分析 设出直线与椭圆的两个交点A,B的坐标及AB的中点的坐标,利用点差法结合直线斜率得到AB中点所满足的函数关系式.
解答 解:设直线l交椭圆与A(x1,y1),B(x2,y2)两点,AB的中点为(x0,y0),
则代入,作差得:$\frac{{2x}_{0}({x}_{1}-{x}_{2})}{3}$+2y0(y1-y2)=0,①
∵kAB=$\frac{{y}_{0}}{{x}_{0}+1}$②,
①②整理得:x02+x0+3y02=0,即x2+x+3y2=0.
∴弦的中点的轨迹方程x2+x+3y2=0.
故答案为:x2+x+3y2=0.
点评 本题考查了轨迹方程的求法,训练了点差法,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.用数学归纳法证明$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{13}{24}$,由n=k到n=k+1左边需添加的项为( )
| A. | $\frac{1}{2(k+1)}$ | B. | $\frac{1}{2k+1}+\frac{1}{2k+2}-\frac{1}{k+1}$ | ||
| C. | $\frac{1}{2k+1}+\frac{1}{2k+2}+\frac{1}{k+1}$ | D. | $\frac{1}{2k+1}+\frac{1}{2k+2}$ |
4.已知定义在R上的函数$f(x)={(\frac{1}{2})^{|x-m|}}-1$(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
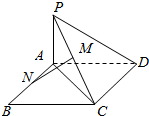 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.