题目内容
 在四棱锥O-ABCD中,底面ABCD为菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:
在四棱锥O-ABCD中,底面ABCD为菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:(1)平面BDO⊥平面ACO;
(2)EF∥平面OCD.
分析:(1)证明平面BDO⊥平面ACO,只需证明平面BD0内的直线BD,垂直平面ACO内的两条相交直线OA、AC即可;
(2)取OD中点M,连接KM、CM,证明EF平行平面OCD内的直线CM,即可证明EF∥平面OCD.
(2)取OD中点M,连接KM、CM,证明EF平行平面OCD内的直线CM,即可证明EF∥平面OCD.
解答: 证明:(1)∵OA⊥平面ABCD,BD?平面ABCD,所以OA⊥BD,
证明:(1)∵OA⊥平面ABCD,BD?平面ABCD,所以OA⊥BD,
∵ABCD是菱形,∴AC⊥BD,又OA∩AC=A,
∴BD⊥平面OAC,
又∵BD?平面OBD,∴平面BD0⊥平面ACO.
(2)取OD中点M,连接KM、CM,则ME∥AD,ME=
AD,
∵ABCD是菱形,∴AD∥BC,AD=BC,
∵F为BC的中点,∴CF∥AD,CF=
AD,
∴ME∥CF,ME=CF.
∴四边形EFCM是平行四边形,∴EF∥CM,
∴EF∥平面OCD
 证明:(1)∵OA⊥平面ABCD,BD?平面ABCD,所以OA⊥BD,
证明:(1)∵OA⊥平面ABCD,BD?平面ABCD,所以OA⊥BD,∵ABCD是菱形,∴AC⊥BD,又OA∩AC=A,
∴BD⊥平面OAC,
又∵BD?平面OBD,∴平面BD0⊥平面ACO.
(2)取OD中点M,连接KM、CM,则ME∥AD,ME=
| 1 |
| 2 |
∵ABCD是菱形,∴AD∥BC,AD=BC,
∵F为BC的中点,∴CF∥AD,CF=
| 1 |
| 2 |
∴ME∥CF,ME=CF.
∴四边形EFCM是平行四边形,∴EF∥CM,
∴EF∥平面OCD
点评:本题考查平面与平面垂直的判定,直线与平面平行的判定,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
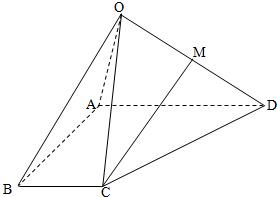 16、如图,在四棱锥O-ABCD中,AD∥BC,AB=AD=2BC,OB=OD,M是OD的中点.
16、如图,在四棱锥O-ABCD中,AD∥BC,AB=AD=2BC,OB=OD,M是OD的中点.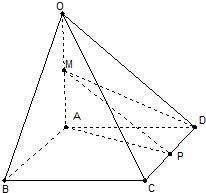 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,P为CD的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,P为CD的中点.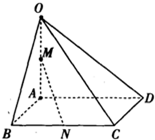 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形, (2009•闸北区二模)如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
(2009•闸北区二模)如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点. 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,