题目内容
已知数列![]() 是等差数列,
是等差数列,![]() 。
。
(1)求数列![]() 的通项
的通项![]() ;
;
(2)设数列![]() 的通项
的通项![]() ,记
,记![]() 是数列
是数列![]() 的前
的前![]() 项和,试比较
项和,试比较![]() 与
与![]() 的大小,并证明你的结论。
的大小,并证明你的结论。
解:(1)设数列![]() 的公差为
的公差为![]() ,
,
由题意得
解得![]() ,∴
,∴![]()
(2)由![]() 知
知
![]()
![]()
∵![]()
因此要比较![]() 与
与![]() 的大小,可先比较
的大小,可先比较![]() 与
与![]() 的大小,
的大小,
取![]() ,有
,有![]()
取![]() ,有
,有![]() ,
,
…
由此推测
![]() >
>![]() ①
①
若①式成立,则由对数函数性质可断定:
![]() >
> ![]()
下面用数学归纳法证明①式.
当![]() 时,已验证①式成立;
时,已验证①式成立;
假设当![]() 时,①式成立,即
时,①式成立,即
![]() >
>![]()
那么,当![]() 时,
时,
![]()
![]()
∵![]()
![]()
∴![]()
∴![]()
∴当![]() 时,①式也成立。
时,①式也成立。
综上知,①式对任何正整数![]() 都成立。
都成立。
由此证得,![]() >
> ![]() 。
。

练习册系列答案
相关题目
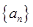 是等差数列,若
是等差数列,若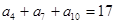 ,
, ,且
,且 ,则
,则 _________.
_________. 是等差数列,
是等差数列, ,则首项
,则首项 .
. 是等差数列,
是等差数列,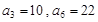 ,数列
,数列 的前n项和是
的前n项和是 ,且
,且 .
. 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 .
的值为 . }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5; }满足:
}满足: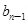 =
= (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1. =
= (n∈N﹡),若{
(n∈N﹡),若{ ,求
,求