题目内容
已知函数
 ,
, 为
为 的导数.
的导数.
(1)当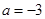 时,求
时,求 的单调区间和极值;
的单调区间和极值;
(2)设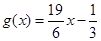 ,是否存在实数
,是否存在实数 ,对于任意的
,对于任意的 ,存在
,存在 ,使得
,使得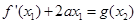 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(1) 在
在 单调递减,在
单调递减,在 单调递增,
单调递增, 极大=
极大=
 极小=
极小=
(2)存在 符合要求
符合要求
解析试题分析:(1)当 时,
时, ,
, ,
,
令 得:
得: 、
、 , ……2分
, ……2分
所以 在
在 单调递减,在
单调递减,在 单调递增, ……4分
单调递增, ……4分
所以 极大=
极大=
 极小=
极小= ……6分
……6分
(2)在 上
上 是增函数,故对于
是增函数,故对于 ,
, .
.
设 .
. ,
,
由 ,得
,得 . ……8分
. ……8分
要使对于任意的 ,存在
,存在 使得
使得 成立,只需在
成立,只需在 上,
上,
- ,
,
在 上
上 ;在
;在 上
上 ,
,
所以 时,
时, 有极小值
有极小值 ……10分
……10分
又 ,
,
因为在 上
上 只有一个极小值,故
只有一个极小值,故 的最小值为
的最小值为 ……12分
……12分  解得
解得 . ……14分
. ……14分
考点:本小题主要考查用导数研究函数的单调性、极值、最值及探究性问题的求解.
点评:导数是研究函数性质的主要依据,研究性质时一定不要忘记考虑函数的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
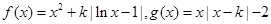 ,其中
,其中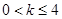 .(1) 讨论函数
.(1) 讨论函数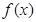 的单调性,并求出
的单调性,并求出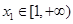 ,都存在
,都存在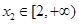 ,使得
,使得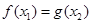 ,求实数
,求实数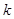 的取值范围.
的取值范围.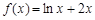 ,
,
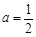 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: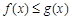 .
.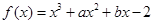 的图象过点
的图象过点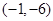 ,且函数
,且函数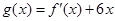 的图象关于
的图象关于 轴对称;
轴对称;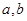 的值及函数
的值及函数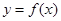 的单调区间;
的单调区间;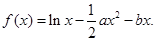
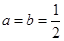 时,求函数
时,求函数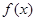 的最大值;
的最大值;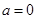 ,
,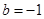 ,方程
,方程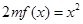 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.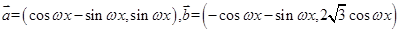 ,设函数
,设函数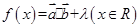 的图象关于直线
的图象关于直线 =π对称,其中
=π对称,其中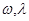 为常数,且
为常数,且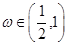 .
. 的最小正周期;
的最小正周期;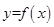 的图象经过点
的图象经过点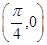 ,求函数
,求函数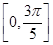 上的取值范围.
上的取值范围.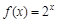 ,
,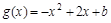
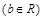 ,记
,记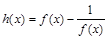 。
。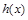 的奇偶性,并证明;
的奇偶性,并证明;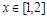 ,都存在
,都存在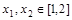 ,使得
,使得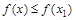 ,
,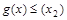 .若
.若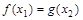 ,求实数
,求实数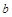 的值;
的值;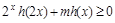 对于一切
对于一切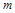 的取值范围.
的取值范围. 是定义在R上的奇函数,且对任意
是定义在R上的奇函数,且对任意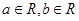 ,当
,当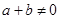 时,都有
时,都有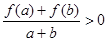 .
.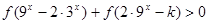 对任意
对任意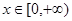 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.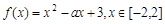 。
。 在
在 上的最小值是
上的最小值是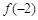 ,试解不等式
,试解不等式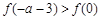 ;
;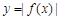 在
在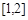 上单调递增,试求实数
上单调递增,试求实数 的取值范围。
的取值范围。