题目内容
已知抛物线方程为 ,直线
,直线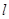 的方程为
的方程为 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为 ,P到直线
,P到直线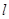 的距离为
的距离为 ,则
,则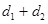 的最小值为( )
的最小值为( )
A. | B. | C.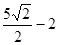 | D. |
D
解析试题分析:如图,可知抛物线焦点F(2,0),准线为x=-1,根据抛物线的定义,∴d1+d2=PM+PN-1=PM+PF-1≥FM-1≥d-1,d为F到l的距离,d= ,∴d1+d2的最小值为
,∴d1+d2的最小值为 .
.
考点:抛物线的定义求线段和差最值问题.

练习册系列答案
相关题目
设双曲线 ,离心率
,离心率 ,右焦点
,右焦点 .方程
.方程 的两个实数根分别为
的两个实数根分别为 ,则点
,则点 与圆
与圆 的位置关系( )
的位置关系( )
| A.在圆外 | B.在圆上 | C.在圆内 | D.不确定 |
设F(1,0),M点在x轴上,P点在y轴上,且 =2
=2 ,
, ⊥
⊥ ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )
| A.y2=2x | B.y2=4x |
C.y2= x x | D.y2= x x |
若双曲线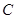 :
: 与抛物线
与抛物线 的准线交于
的准线交于 两点,且
两点,且 ,则
,则 的值是( )
的值是( )
| A.1 | B. | C.4 | D.13 |
[2013·湖北高考]已知0<θ< ,则双曲线C1:
,则双曲线C1: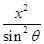 -
- =1与C2:
=1与C2: -
-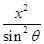 =1的( )
=1的( )
| A.实轴长相等 | B.虚轴长相等 |
| C.离心率相等 | D.焦距相等 |
 的左右焦点为F1,F2离心率为
的左右焦点为F1,F2离心率为 ,过F2的直线l交C与A,B两点,若△AF1B的周长为
,过F2的直线l交C与A,B两点,若△AF1B的周长为 ,则C的方程为( )
,则C的方程为( )


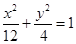
 ,定义
,定义 的算法原理如右侧程序框图所示.设
的算法原理如右侧程序框图所示.设 为函数
为函数 的最大值,
的最大值, 为双曲线
为双曲线 的离心率,则计算机执行该运算后输出的结果是( )
的离心率,则计算机执行该运算后输出的结果是( )




 的焦点相同,且椭圆上任意一点到两焦点的距离之和为
的焦点相同,且椭圆上任意一点到两焦点的距离之和为 ,那么椭圆的离心率等于( )
,那么椭圆的离心率等于( )



 的左右焦点为
的左右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直于直线
垂直于直线 的垂直平分线与
的垂直平分线与 ,若
,若 是
是 ,则
,则 的取值范围是( )
的取值范围是( )

