题目内容
已知函数
，对于满足
的任意
，下列结论：
（1）
；（2）
（3）
； （4）
其中正确结论的序号是（ ）
| A．（1）（2） | B．（1）（3） | C．（2）（4） | D．(3)(4) |
C
解析试题分析：因为函数，所以函数在定义域内单调递增，对于满足，可得
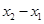与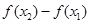
同号，所以（1）不正确.所以排除A,B两选项.由可得
.因为函数递增，所以（2）成立.(3)不成立，斜率不可能都大于1，函数是下凹的图像，所以（4）正确.故选C.
考点：1.函数的单调性.2.函数的斜率公式.3.凹凸函数的性质.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在
上的可导函数
的导函数为
，满足
，且
则不等式
的解集为（ ）
A． | B． | C． | D． |
定义一种运算
，则函数
的值域为
A． | B． | C． | D． |
下列四组函数中，表示为同一函数的是（ ）
A． | B． 与 |
C． | D． |
已知函数
，那么
的值是（ ）
A． | B． | C． | D． |
定义在R上的函数
满足：的图像关于
轴对称，并且对任意的
有
，则当
时，有( )
A． | B． |
C． | D． |
函数
，设
，若
，
的取值范围是( )
A． | B． | C． | D． |
方程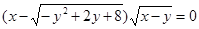
表示的曲线为 ( )
| A．一条直线和一个圆 | B．一条射线与半圆 |
| C．一条射线与一段劣弧 | D．一条线段与一段劣弧 |
若y＝f(x)既是周期函数，又是奇函数，则其导函数y＝f′(x)( )．
| A．既是周期函数，又是奇函数 |
| B．既是周期函数，又是偶函数 |
| C．不是周期函数，但是奇函数 |
| D．不是周期函数，但是偶函数 |