Question

【题目】若函数对定义域内的每一个值，在其定义域内都存在唯一的，使成立，则称该函数为“依赖函数”.

（1）判断函数是否为“依赖函数”，并说明理由；

（2）若函数在定义域（）上为“依赖函数”，求的取值范围；

（3）已知函数在定义域上为“依赖函数”.若存在实数，使得对任意的，不等式恒成立，求实数的最大值.

Answer 1

【答案】（1）不是“依赖函数”，见解析；（2）（3）实数的最大值为.

【解析】

（1）利用时，不可能成立，判断出不是“依赖函数”.

（2）结合指数型函数的单调性，利用“依赖函数”的定义，求得，由此将转化为，然后结合二次函数的单调性，求得的取值范围.

（3）根据与区间的位置关系进行分类讨论，结合二次函数的性质以及“依赖函数”的定义，求得的值.由此化简不等式为以为主变量的形式.利用判别式得到，结合存在性问题，由的最大值，求得的取值范围，从而求得的最大值.

（1）对于函数的定义域内存在，

则，无解，故不是“依赖函数”.

（2）因为在递增，故，即，

由，故，得，

从而在上单调递增，故，

（3）①若，故在上最小值为0，此时不存在，舍去；

②若故在上单调递减，

∴，解得（舍）或.

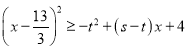∴存在，使得对任意的，有不等式都成立，

即恒成立，由，

得，由，可得，

又在单调递减，故当时，，

从而，解得，

综上，故实数的最大值为.