题目内容
ABC—A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点.
(1)求证:AB1D⊥平面ABB1A1;
(2)求点C到平面AB1D的距离;
(3)求平面AB1D与平面ABC所成二面角(锐角)的大小.
解:(1)取AB1中点M, 则
![]() .
.
又![]() ,
,
两式相加可得![]() .
.
由于![]() ,
,
![]()
![]() .
.
∴DM⊥AA1.又DM⊥AB,
∴DM⊥平面ABB1A1, 而DM![]() 平面AB1D.
平面AB1D.
∴平面AB1D⊥平面ABB1A1.
(2)一方面A1B⊥DM, 另一方面![]() ,
,
∴A1B⊥AB1.∴A1B⊥平面AB1D.
∴A1B是平面AB1D的法向量.
∴C点到平面AB1D的距离
 .
.
(3)平面ABC的法向量为![]() , 而平面AB1D的法向量是
, 而平面AB1D的法向量是![]() , 故所求二面角θ为
, 故所求二面角θ为
 ,
,
∴θ=45°.

练习册系列答案
相关题目
 如图,三棱柱ABC-A1B1C1的侧棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB中点,AC=BC=1,AA1=1.
如图,三棱柱ABC-A1B1C1的侧棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB中点,AC=BC=1,AA1=1.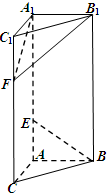 (2013•闵行区二模)如图,在直三棱柱ABC-A1B1C1中,
(2013•闵行区二模)如图,在直三棱柱ABC-A1B1C1中,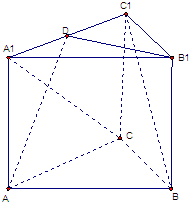 (2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=
(2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=