题目内容
如图,一架直升飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为30°,经过2分钟后又看到山顶的俯角为75°,求山顶的海拔高度.
【答案】分析:根据题意求得∠APB和AB的长,然后利用正弦定理求得BP,最后利用BP•sin75°求得问题的答案.
解答:解:在△ABP中,∠BAP=30°,∠APB=75°-30°=45°,AB=180× =6.
=6.
根据正弦定理, =
= ,
, =
= ,BP=3
,BP=3 .
.
BP•sin75°=3 ×sin(45°+30°)=
×sin(45°+30°)= .
.
所以,山顶P的海拔高度为h=10- =
= (千米).
(千米).
点评:本题主要考查了解三角形问题的应用.注意把实际问题与三角函数的知识相联系,建立相应的数学模型.
解答:解:在△ABP中,∠BAP=30°,∠APB=75°-30°=45°,AB=180×
 =6.
=6.根据正弦定理,
 =
= ,
, =
= ,BP=3
,BP=3 .
.BP•sin75°=3
 ×sin(45°+30°)=
×sin(45°+30°)= .
.所以,山顶P的海拔高度为h=10-
 =
= (千米).
(千米).点评:本题主要考查了解三角形问题的应用.注意把实际问题与三角函数的知识相联系,建立相应的数学模型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,一架直升飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为30°,经过2分钟后又看到山顶的俯角为75°,求山顶的海拔高度.
如图,一架直升飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为30°,经过2分钟后又看到山顶的俯角为75°,求山顶的海拔高度.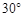 ,经过2分钟后又看到山顶的俯角为
,经过2分钟后又看到山顶的俯角为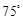 ,求山顶的海拔高度.
,求山顶的海拔高度. 
 如图,一架直升飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为30°,经过2分钟后又看到山顶的俯角为75°,求山顶的海拔高度.
如图,一架直升飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为30°,经过2分钟后又看到山顶的俯角为75°,求山顶的海拔高度.