题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值,并指出
的最小值,并指出![]() 最小时对应的点
最小时对应的点![]() 的坐标.
的坐标.
【答案】(1)2;(2)![]() 有最小值4,此时
有最小值4,此时![]() .
.
【解析】
(1)先求出以点![]() 为切点的抛物线的切线
为切点的抛物线的切线![]() 方程,得出
方程,得出![]() ,
,![]() 利用面积求出
利用面积求出![]() 点的纵坐标,然后求出
点的纵坐标,然后求出![]() 。
。
(2)先分别写出直线PA,PB方程,利用都过点P写出直线![]() ,代入抛物线方程利用弦长公式求出
,代入抛物线方程利用弦长公式求出![]() ,及点
,及点![]() 到直线
到直线![]() 的距离,写出
的距离,写出![]() 表达式及最值。
表达式及最值。
(1)设![]() ,
,![]() ,
,![]() ,则
,则![]() ,抛物线方程写成
,抛物线方程写成![]() ,
,![]() ,则以点
,则以点![]() 为切点的抛物线的切线
为切点的抛物线的切线![]() 的方程为:
的方程为:![]() ,又
,又![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,故
,故![]()
![]() ,∴
,∴![]() ,
,![]() ,从而
,从而![]() .
.
(2)由(1)知![]() ,即:
,即:![]() ,同理
,同理![]() ,由直线
,由直线![]() ,
,![]() 都过点
都过点![]() ,即
,即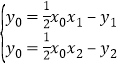 ,则点
,则点![]() ,
,![]() 的坐标都满足方程
的坐标都满足方程![]() ,
,
即直线![]() 的方程为:
的方程为:![]() ,又由直线
,又由直线![]() 过点
过点![]() ,∴
,∴![]() ,
,
联立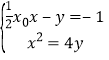 得
得![]() ,
,
![]()
![]()
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离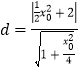 ,
,
![]()
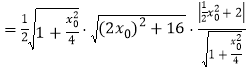
![]()
![]() ,
,
当且仅当时![]() ,
,![]() 有最小值4,此时
有最小值4,此时![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目