题目内容
已知椭圆E的中心在坐标原点O,经过两点 圆C以点(2,0)为圆心,椭圆的短半袖长为半径.
圆C以点(2,0)为圆心,椭圆的短半袖长为半径.
(1)求椭圆E的标准方程;
(2)若点P是圆C上的一个动点,求 的取值范围.
的取值范围.
解:(1)设椭圆E的标准方程为mx2+ny2=1(m>0,n>0,且m≠n).
因为 在椭圆E上,所以
在椭圆E上,所以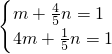
解得 ,满足条件
,满足条件
所以所求椭圆E的标准方程为
(2)由(1)知椭圆的短半轴长为1,所以圆心坐标为(2,0),半径r=1,
故圆C的方程为(x-2)2+y2=1.
设P(x,y),则 ,
,
所以
因为(x-2)2+y2=1,所以(x-2)2≤1,即-1≤x-2≤1,得1≤x≤3.
所以-1≤2x-3≤3,即 的取值范围为[-1,3].
的取值范围为[-1,3].
分析:(1)设出椭圆的标准方程把A,B点的坐标代入即可求得m和n,则椭圆的方程可得.
(2)根据椭圆的短半轴的长求得圆心的坐标和半径,进而可得圆的方程,设出P的坐标,则可分别表示出 和
和 ,进而求得
,进而求得 的表达式,进而根据圆方程确定x的范围,进而求得
的表达式,进而根据圆方程确定x的范围,进而求得 的取值范围.
的取值范围.
点评:本题主要考查了椭圆的应用.考查了学生综合分析问题的能力.
因为
 在椭圆E上,所以
在椭圆E上,所以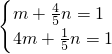
解得
 ,满足条件
,满足条件所以所求椭圆E的标准方程为

(2)由(1)知椭圆的短半轴长为1,所以圆心坐标为(2,0),半径r=1,
故圆C的方程为(x-2)2+y2=1.
设P(x,y),则
 ,
,所以

因为(x-2)2+y2=1,所以(x-2)2≤1,即-1≤x-2≤1,得1≤x≤3.
所以-1≤2x-3≤3,即
 的取值范围为[-1,3].
的取值范围为[-1,3].分析:(1)设出椭圆的标准方程把A,B点的坐标代入即可求得m和n,则椭圆的方程可得.
(2)根据椭圆的短半轴的长求得圆心的坐标和半径,进而可得圆的方程,设出P的坐标,则可分别表示出
 和
和 ,进而求得
,进而求得 的表达式,进而根据圆方程确定x的范围,进而求得
的表达式,进而根据圆方程确定x的范围,进而求得 的取值范围.
的取值范围.点评:本题主要考查了椭圆的应用.考查了学生综合分析问题的能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
欲知作者的性别是否与读者的性别有关,某出版公司派人员到各书店随机调查了500位买书的顾客,结果如下:
作家 读者 | 男作家 | 女作家 | 合计 |
| 男读者 | 142 | 122 | 264 |
| 女读者 | 103 | 133 | 236 |
| 合计 | 245 | 255 | 500 |
 的一条渐近线方程为y=
的一条渐近线方程为y= ,则此双曲线的离心率为
,则此双曲线的离心率为



 的是
的是 ,且
,且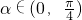 ,则sinα-cosα等于
,则sinα-cosα等于







