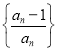
题目内容
【题目】对于项数为m（
且
）的有穷正整数数列
，记
，即
为
中的最小值，设由
组成的数列
称为的“新型数列”.
（1）若数列为2019，2020，2019，2018，2017，请写出的“新型数列”的所有项；
（2）若数列满足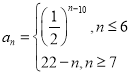
，且其对应的“新型数列”项数
，求的所有项的和；
（3）若数列的各项互不相等且所有项的和等于所有项的积，求符合条件的及其对应的“新型数列”.
【答案】（1）数列
为2019，2019，2019，2018，2017（2）
（3）满足题意的数列
：
.所以对应的“新型数列”分别为：
.
【解析】
(1)根据
的定义直接写出
的所有项；(2)首先推出
关于n递减，则中共21项且各项分别与中各项相同，相加利用等比数列的前n项和公式即可得解.(3)先不妨设数列单调递增，分
、
、
三种情况讨论，求出满足题意的数列，进而求得对应的“新型数列”.
解：（1）数列为2019，2019，2019，2018，2017；
（2）由已知得：当
时，关于n递减；当
时，关于n递减，
又
时，关于n递减.
，
.
又
，
.
共21项且各项分别与中各项相同，
其和为
.
（3）先不妨设数列单调递增，
当时，
，
，
，此时无解，不满足题意；
当时，由
得
，
，又
，
，代入原式得
.
当时，
，
而
，矛盾，
所以不存在满足题意的数列.
综上，满足题意的数列：.
所以对应的“新型数列”分别为：.
练习册系列答案
相关题目
