Question

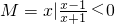，P={x|（x-b）²＜a}．若“a=1”是“M∩P≠Ф”的充分条件，则b的取值范围是

1. A.
   -2≤b＜0
2. B.
   0＜b≤2
3. C.
   -3＜b＜-1
4. D.
   -2＜b＜2

Answer 1

D
分析：求出M，P两个集合，通过“a=1”是“M∩P≠Ф”的充分条件，推出-1≤b-1＜1或-1＜b+1≤1，得到选项．
解答：由已知M=（-1，1），P=（b-a，a+b）
∵a=1
∴P=（b-1，1+b）
∵M∩P≠∅
∴-1≤b-1＜1或-1＜b+1≤1
∴0≤b＜2或-2＜b≤0，
以上每步可逆，故a=1时，M∩P≠∅的充分条件是0≤b＜2或-2＜b≤0即b∈（-2，2）；
故选D．
点评：本题考查充分条件与集合的交并，其中正确理解若“a=1”，是M∩P≠∅的充分条件是关键．