Question

在直角坐标系xOy中,椭圆C₁: =1 (a＞b＞0)的左、右焦点分别为F₁、F₂.F₂也是抛物线C₂：y²=4x的焦点，点M为C₁与C₂在第一象限的交点，且|MF₂|=.

（1）求C₁的方程；

（2）平面上的点N满足=+，直线l∥MN，且与C₁交于A、B两点，若·=0，求直线l的方程.

Answer 1

（1）（2）直线l的方程为y=x-2,或y=x+2

解析:

(1)由C₂:y²=4x,知F₂(1,0),

设M(x₁,y₁),M在C₂上,

因为|MF₂|=,所以x₁+1=,

得x₁=,y₁=.所以M.

M在C₁上,且椭圆C₁的半焦距c=1,

于是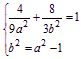

消去b²并整理得9a⁴-37a²+4=0.

解得a=2(a=不合题意,舍去).

故b²=4-1=3.

故椭圆C₁的方程为.

(2)由=+,知四边形MF₁NF₂是平行四边形,其中心为坐标原点O,

因为l∥MN,所以l与OM的斜率相同.

故l的斜率k==.

设l的方程为y=(x-m).

由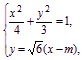消去y并整理得

9x²-16mx+8m²-4=0.

设A(x₁,y₁),B(x₂,y₂),

则x₁+x₂=,x₁x₂=.

因为⊥,所以x₁x₂+y₁y₂=0.

所以x₁x₂+y₁y₂=x₁x₂+6(x₁-m)(x₂-m)

=7x₁x₂-6m(x₁+x₂)+6m²

=7·-6m·+6m²=(14m²-28)=0.

所以m=±.此时Δ=(16m)²-4×9(8m²-4)＞0.

故所求直线l的方程为y=x-2,或y=x+2.