题目内容
 和
和 是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是 ________
是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是 ________
(1) +
+ 和
和 -
- ;(2)3
;(2)3 -2
-2 和4
和4 -6
-6 ;
;
(3) +2
+2 和
和 +2
+2 ;(4)
;(4) 和
和 +
+ .
.
解:因为(1)中的向量  +
+ 和
和 -
- 不共线,故可以作为一组基底.
不共线,故可以作为一组基底.
因为(2)中的向量 3 -2
-2 和4
和4 -6
-6 满足4
满足4 -6
-6 =-2(3
=-2(3 -2
-2 ),是一组共线向量,故不可作为一组基底.
),是一组共线向量,故不可作为一组基底.
因为(3)中的向量 +2
+2 和
和 +2
+2 是两个不共线的向量,故可以作为一组基底.
是两个不共线的向量,故可以作为一组基底.
因为(4)中的向量 和
和 +
+ 是一组不共线的向量,故可以作为一组基底.
是一组不共线的向量,故可以作为一组基底.
综上,只有(2)中的向量不可作为一组基底,
故答案为 (2).
分析:首先考查各个选项中的两个向量是否是共线向量,共线向量,不可作为一组基底,只有不共线的两个向量才可作为一组基底.
点评:本题考查平面向量的基本定理及其意义,共线向量与基底的定义.
 +
+ 和
和 -
- 不共线,故可以作为一组基底.
不共线,故可以作为一组基底.因为(2)中的向量 3
 -2
-2 和4
和4 -6
-6 满足4
满足4 -6
-6 =-2(3
=-2(3 -2
-2 ),是一组共线向量,故不可作为一组基底.
),是一组共线向量,故不可作为一组基底.因为(3)中的向量
 +2
+2 和
和 +2
+2 是两个不共线的向量,故可以作为一组基底.
是两个不共线的向量,故可以作为一组基底.因为(4)中的向量
 和
和 +
+ 是一组不共线的向量,故可以作为一组基底.
是一组不共线的向量,故可以作为一组基底.综上,只有(2)中的向量不可作为一组基底,
故答案为 (2).
分析:首先考查各个选项中的两个向量是否是共线向量,共线向量,不可作为一组基底,只有不共线的两个向量才可作为一组基底.
点评:本题考查平面向量的基本定理及其意义,共线向量与基底的定义.

练习册系列答案
相关题目
 和
和 是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是( )
是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是( ) -2
-2 和4
和4 -6
-6
 +
+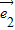 和
和 -
-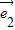
 +2
+2 和
和 +2
+2
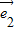 和
和 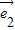 +
+