题目内容
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为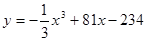 ,则使该生产厂家获得最大年利润的年产量为( )
,则使该生产厂家获得最大年利润的年产量为( )
| A. 13万件 | B. 11万件 | C. 9万件 | D. 7万件 |
C
解析试题分析:令导数y′=-x2+81>0,解得0<x<9;
令导数y′=-x2+81<0,解得x>9,
所以函数y=- x3+81x-234在区间(0,9)上是增函数,
x3+81x-234在区间(0,9)上是增函数,
在区间(9,+∞)上是减函数,所以在x=9处取极大值,也是最大值,故选C
考点:本题主要考查了导数在实际问题中的应用,属基础题.
点评:解决该试题的关键是由题意先对函数y进行求导,解出极值点,然后再根据函数的定义域,把极值点和区间端点值代入已知函数,比较函数值的大小,求出最大值即最大年利润的年产量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知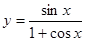 ,
,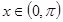 .当
.当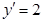 时,
时,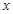 等于
等于
A.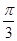 | B.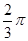 | C.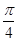 | D.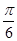 |
若点P是曲线y=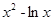 上任意一点,则点P到直线y=x-2的最小距离是 ( )
上任意一点,则点P到直线y=x-2的最小距离是 ( )
A.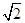 | B.1 | C.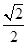 | D.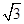 |
曲线y= 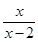 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为
| A.y=x-2 | B.y=-3x+2 | C.y=2x-3 | D.y=-2x+1 |
已知R上可导函数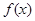 的图象如图所示,则不等式
的图象如图所示,则不等式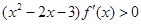 的解集为( )
的解集为( )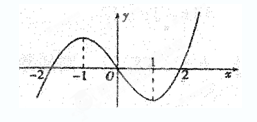
A. |
B.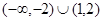 |
C.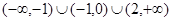 |
D.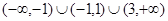 |
若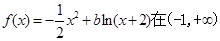 上是减函数,则
上是减函数,则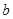 的取值范围是( )
的取值范围是( )
A.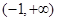 | B.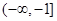 | C.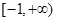 | D.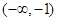 |
函数 有( )
有( )
| A.极大值5,极小值-27 | B.极大值5,极小值-11 |
| C.极大值5,无极小值 | D.极小值-27,无极大值 |
已知定义在R上的奇函数 ,设其导函数
,设其导函数 ,当
,当 时,恒有
时,恒有 ,则满足
,则满足 的实数
的实数 的取值范围是( )
的取值范围是( )
| A.(-1,2) | B. | C. | D.(-2,1) |
 是函数
是函数 的导函数,将
的导函数,将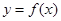 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )