题目内容
函数y=f(x)对于任意正实数x、y,都有f(xy)=f(x)•f(y),当x>1时,0<f(x)<1,且f(2)= .
.(1)求证:
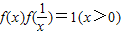 ;
;(2)判断f(x)在(0,+∞)的单调性;并证明;
(3)若f(m)=3,求正实数m的值.
【答案】分析:(1)令x=1,y=2,结合f(2)= 可求得f(1)=1,再令y=
可求得f(1)=1,再令y=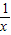 ,可证明
,可证明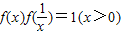 ;
;
(2)任取x1,x2∈(0,+∞),且x1<x2,则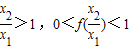 ,作差f(x1)-f(x2)=f(x1)[1-f(
,作差f(x1)-f(x2)=f(x1)[1-f(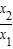 )],结合(1)即可判断f(x)在(0,+∞)上是单调递减性;
)],结合(1)即可判断f(x)在(0,+∞)上是单调递减性;
(3)由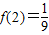 =
=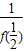 可求得f(
可求得f( )=3,结合(2)f(x)在(0,+∞)上是单调递减函数可求m的值.
)=3,结合(2)f(x)在(0,+∞)上是单调递减函数可求m的值.
解答:证明:(1)令x=1,y=2,得f(2)=f(1)f(2),又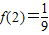 ,
,
∴f(1)=1,…(2分)
令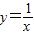 ,得
,得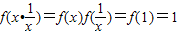 ; …(4分)
; …(4分)
(2)任取x1,x2∈(0,+∞),且x1<x2,则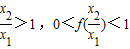 ,
,
∴f(x1)-f(x2)=f(x1)-f(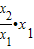 )=f(x1)-f(
)=f(x1)-f(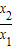 )f(x1)=f(x1)[1-f(
)f(x1)=f(x1)[1-f(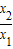 )],…(7分)
)],…(7分)
而当x>0时,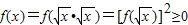 ,且由(1)可知,
,且由(1)可知,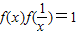 ,f(x)≠0,
,f(x)≠0,
则当x>0时,f(x)>0,
∴f(x1)>0,1-f(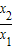 )>0,
)>0,
∴f(x1)-f(x2)>0,
则f(x)在(0,+∞)上是单调递减函数;…(10分)
(3)∵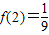 ,
,
∴f( )=
)=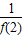 =9,
=9,
又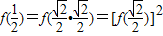 ,且
,且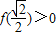 ,
,
∴f(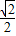 )=3,…(13分)
)=3,…(13分)
∵f(x)在(0,+∞)上是单调递减函数,m是正实数,
∴m=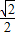 …(16分)
…(16分)
点评:本题考查抽象函数及其用,关键在于对条件及证明过的结论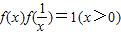 的灵活应用,属于难题.
的灵活应用,属于难题.
 可求得f(1)=1,再令y=
可求得f(1)=1,再令y=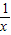 ,可证明
,可证明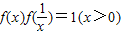 ;
;(2)任取x1,x2∈(0,+∞),且x1<x2,则
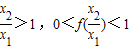 ,作差f(x1)-f(x2)=f(x1)[1-f(
,作差f(x1)-f(x2)=f(x1)[1-f(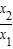 )],结合(1)即可判断f(x)在(0,+∞)上是单调递减性;
)],结合(1)即可判断f(x)在(0,+∞)上是单调递减性;(3)由
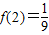 =
=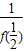 可求得f(
可求得f( )=3,结合(2)f(x)在(0,+∞)上是单调递减函数可求m的值.
)=3,结合(2)f(x)在(0,+∞)上是单调递减函数可求m的值.解答:证明:(1)令x=1,y=2,得f(2)=f(1)f(2),又
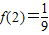 ,
,∴f(1)=1,…(2分)
令
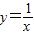 ,得
,得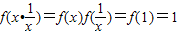 ; …(4分)
; …(4分)(2)任取x1,x2∈(0,+∞),且x1<x2,则
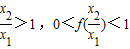 ,
,∴f(x1)-f(x2)=f(x1)-f(
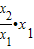 )=f(x1)-f(
)=f(x1)-f(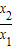 )f(x1)=f(x1)[1-f(
)f(x1)=f(x1)[1-f(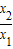 )],…(7分)
)],…(7分)而当x>0时,
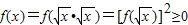 ,且由(1)可知,
,且由(1)可知,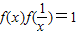 ,f(x)≠0,
,f(x)≠0,则当x>0时,f(x)>0,
∴f(x1)>0,1-f(
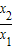 )>0,
)>0,∴f(x1)-f(x2)>0,
则f(x)在(0,+∞)上是单调递减函数;…(10分)
(3)∵
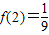 ,
,∴f(
 )=
)=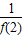 =9,
=9,又
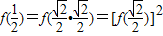 ,且
,且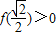 ,
,∴f(
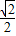 )=3,…(13分)
)=3,…(13分)∵f(x)在(0,+∞)上是单调递减函数,m是正实数,
∴m=
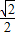 …(16分)
…(16分)点评:本题考查抽象函数及其用,关键在于对条件及证明过的结论
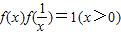 的灵活应用,属于难题.
的灵活应用,属于难题. 
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目