题目内容
(本小题满分12分)
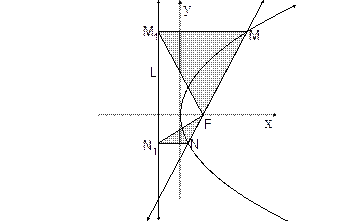
已知直线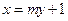 过抛物线
过抛物线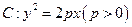 的焦点
的焦点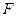 且与抛物线相交于两点
且与抛物线相交于两点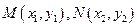 ,自
,自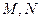 向准线
向准线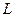
 作垂线,垂足分别为
作垂线,垂足分别为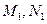 .
.
(Ⅰ)求抛物线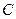 的方程;
的方程;
(Ⅱ)证明:无论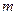 取何实数时,
取何实数时,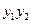 ,
,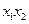 都是定值;
都是定值;
(III)记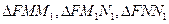 的面积分别为
的面积分别为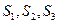 ,试判断
,试判断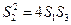 是否成立,并证明你的结论.
是否成立,并证明你的结论.
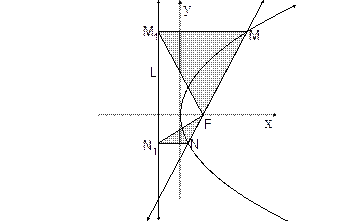
已知直线
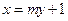 过抛物线
过抛物线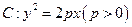 的焦点
的焦点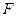 且与抛物线相交于两点
且与抛物线相交于两点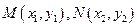 ,自
,自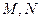 向准线
向准线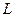
 作垂线,垂足分别为
作垂线,垂足分别为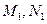 .
.(Ⅰ)求抛物线
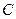 的方程;
的方程;(Ⅱ)证明:无论
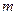 取何实数时,
取何实数时,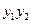 ,
,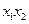 都是定值;
都是定值;(III)记
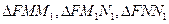 的面积分别为
的面积分别为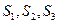 ,试判断
,试判断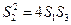 是否成立,并证明你的结论.
是否成立,并证明你的结论.(1)
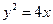
(2)略
(3)
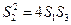
(Ⅰ)解:由条件知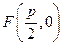 在直线
在直线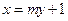 上,即
上,即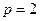 ,
,

所以抛物线 的方程为
的方程为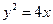 .………………2分
.………………2分
(Ⅱ) 由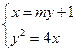 得
得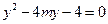 .………………3分
.………………3分
则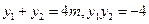 .………………4分
.………………4分
则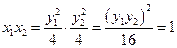 ,即有定值
,即有定值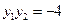 ,
,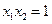 .………………6分
.………………6分
(III) 根据条件有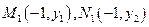 .
.
由抛物线的定义得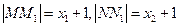 ,………………7分
,………………7分
于是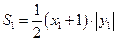 ,
,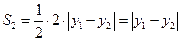 ,.
,.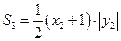 ……………8分
……………8分
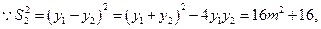 ………………9分
………………9分
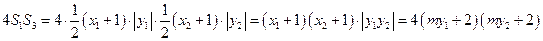
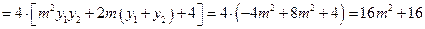 ,
,
则有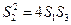 .………………12分
.………………12分
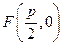 在直线
在直线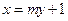 上,即
上,即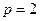 ,
,
所以抛物线
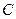 的方程为
的方程为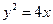 .………………2分
.………………2分(Ⅱ) 由
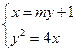 得
得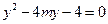 .………………3分
.………………3分则
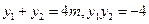 .………………4分
.………………4分则
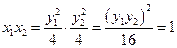 ,即有定值
,即有定值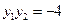 ,
,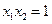 .………………6分
.………………6分(III) 根据条件有
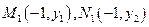 .
.由抛物线的定义得
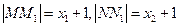 ,………………7分
,………………7分于是
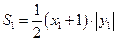 ,
,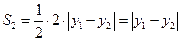 ,.
,.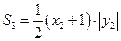 ……………8分
……………8分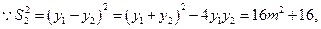 ………………9分
………………9分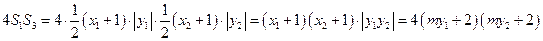
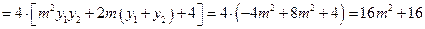 ,
,则有
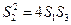 .………………12分
.………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
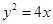 的焦点坐标为 ( ■ )
的焦点坐标为 ( ■ )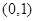
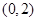
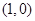
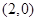
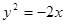
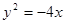
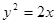
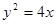
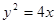 的焦点作直线与抛物线交于
的焦点作直线与抛物线交于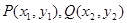 两点,若
两点,若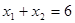 ,则
,则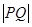 的值为
的值为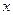 轴上的抛物线与
轴上的抛物线与 直线
直线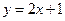 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=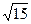 ,求抛物线的方程
,求抛物线的方程

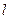 时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?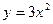 的焦点坐标是_
的焦点坐标是_ ___________________.
___________________.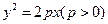 ,过定点
,过定点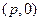 作两条互相垂直的直线
作两条互相垂直的直线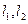 ,若
,若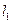 与抛物线交于点
与抛物线交于点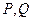 ,
,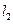 与抛物线交于
与抛物线交于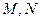 点,
点,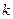 .某同学已正确求得弦
.某同学已正确求得弦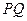 的中点坐标为
的中点坐标为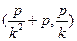 ,请写出弦
,请写出弦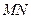 的中点坐标 .
的中点坐标 .