题目内容
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
(Ⅰ)由f(x)的图象经过P(0,2),知d=2,则
f(x)=x3+bx2+cx+2,f¢(x)=3x2+2bx+c,
由在M(-1,f(-1))处的切线方程是6x-y+7=0,知-6-f(-1)+7=0,即f(-1)=1,且f¢(-1)=6,
∴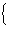
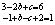 ,即
,即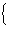
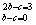 ,解得b=c=-3,
,解得b=c=-3,
故所求的解析式是f(x)=x3-3x2-3x+2.
(Ⅱ)f¢(x)=3x2-6x-3,令3x2-6x-3=0,即x2-2x-1=0,
解得x1=1-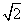 ,x2=1+
,x2=1+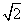 ,当x<1-
,当x<1-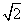 或x>1+
或x>1+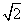 时,f¢(x)>0;
时,f¢(x)>0;
当1-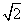 <x<1+
<x<1+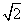 时,f¢(x)<0,
时,f¢(x)<0,
故f(x)=x3-3x2-3x+2在(-∞,1-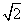 )内是增函数,在(1-
)内是增函数,在(1-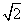 ,1+
,1+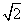 )内是减函数,在(1+
)内是减函数,在(1+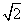 ,+∞)内是增函数.
,+∞)内是增函数.

练习册系列答案
相关题目
 的焦点为
的焦点为 ,准线为
,准线为 ,经过
,经过 的直线与抛物线在
的直线与抛物线在 轴上方的部分相交于点
轴上方的部分相交于点 ,
, ,垂足为
,垂足为 ,则
,则 的面积是( )
的面积是( ) A.
A. B.
B. C.
C. D.
D.
 的定义域为
的定义域为 ,
,  ,对任意
,对任意 ,
, ,则
,则
 ,1) B.(
,1) B.( ) C.(
) C.( ,
, 在点
在点  处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( ) B
B  C
C  D
D 
 ,若函数
,若函数 有大于零的极值点,则实数
有大于零的极值点,则实数 的取值范围是 .
的取值范围是 . )在第四象限,则角
)在第四象限,则角 在( )
在( ) 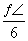 )的图象上所有点的( )
)的图象上所有点的( )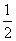 (纵坐标不变),所得图象再向左平移
(纵坐标不变),所得图象再向左平移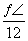 个单位长度
个单位长度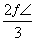 个单位长度
个单位长度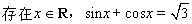 ”,则Øp是假命题
”,则Øp是假命题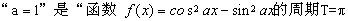 ”的充分必要条件
”的充分必要条件 的否定是:“
的否定是:“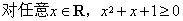 ”
”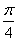 ” 的逆否命题是真命题
” 的逆否命题是真命题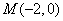 ,
,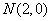 ,
,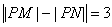 ,则动点
,则动点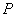 的轨迹是( )21
的轨迹是( )21