题目内容
已知函数f(x)=x2+bsinx-2,(b∈R),且对任意x∈R,有f(-x)=f(x).
(1)求b;
(2)已知g(x)=f(x)+2(x+1)+alnx在区间(0,1)上为单调函数,求实数a的取值范围.
(3)讨论函数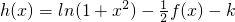 的零点个数?(提示:
的零点个数?(提示: )
)
解:(1)由f(-x)=(-x)2+bsin(-x)-2=f(x)得b=0.…
(2)g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx所以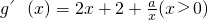 …
…
依题意,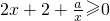 或
或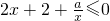 在(0,1)上恒成立…
在(0,1)上恒成立…
即2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立
由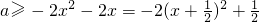 在(0,1)上恒成立,可知a≥0.
在(0,1)上恒成立,可知a≥0.
由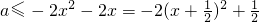 在(0,1)上恒成立,
在(0,1)上恒成立,
可知a≤-4,所以a≥0或a≤-4.…
(3)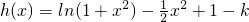 ,令
,令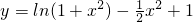 .
.
所以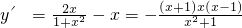 …
…
令y'=0,则x1=-1,x2=0,x3=1,列表如下:
所以当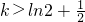 时,函数无零点;
时,函数无零点;
当k<1或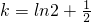 时,函数有两个零点;当k=1时,函数有三个零点.当
时,函数有两个零点;当k=1时,函数有三个零点.当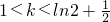 时,函数有四个零点.…
时,函数有四个零点.…
分析:(1)根据f(-x)=f(x)建立等式关系,即可求出b的值;
(2)g(x)=f(x)+2(x+1)+alnx在区间(0,1)上为单调函数,则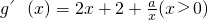 在(0,1)上恒成立,然后将a分离出来,研究不等式另一侧的最值即可求出a的范围;
在(0,1)上恒成立,然后将a分离出来,研究不等式另一侧的最值即可求出a的范围;
(3)令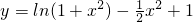 ,研究该函数的单调性和极值,结合图形可判断函数
,研究该函数的单调性和极值,结合图形可判断函数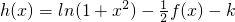 的零点个数.
的零点个数.
点评:本题主要考查了偶函数的性质,以及函数的单调性和极值等有关基础知识,同时考查了恒成立问题,属于中档题.
(2)g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx所以
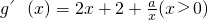 …
…依题意,
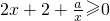 或
或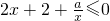 在(0,1)上恒成立…
在(0,1)上恒成立…即2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立
由
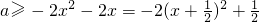 在(0,1)上恒成立,可知a≥0.
在(0,1)上恒成立,可知a≥0.由
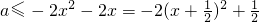 在(0,1)上恒成立,
在(0,1)上恒成立,可知a≤-4,所以a≥0或a≤-4.…
(3)
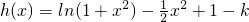 ,令
,令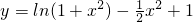 .
.所以
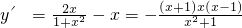 …
…令y'=0,则x1=-1,x2=0,x3=1,列表如下:
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| y' | + | 0 | - | 0 | + | 0 | - |
| h(x) | 单调递增 | 极大值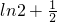 | 单调递减 | 极小值1 | 单调递增 | 极大值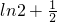 | 单调递减 |
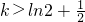 时,函数无零点;
时,函数无零点;当k<1或
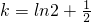 时,函数有两个零点;当k=1时,函数有三个零点.当
时,函数有两个零点;当k=1时,函数有三个零点.当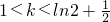 时,函数有四个零点.…
时,函数有四个零点.…分析:(1)根据f(-x)=f(x)建立等式关系,即可求出b的值;
(2)g(x)=f(x)+2(x+1)+alnx在区间(0,1)上为单调函数,则
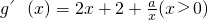 在(0,1)上恒成立,然后将a分离出来,研究不等式另一侧的最值即可求出a的范围;
在(0,1)上恒成立,然后将a分离出来,研究不等式另一侧的最值即可求出a的范围;(3)令
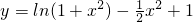 ,研究该函数的单调性和极值,结合图形可判断函数
,研究该函数的单调性和极值,结合图形可判断函数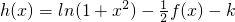 的零点个数.
的零点个数.点评:本题主要考查了偶函数的性质,以及函数的单调性和极值等有关基础知识,同时考查了恒成立问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|