题目内容
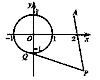
如图，已知圆O
由圆O外一点P（a,b）向圆O引切线PQ，切点为QH满足|PQ|=|PA|。
（1）求实数a、b间满足的等量关系；
（2）求线段PQ长的最小值；
（3）若以P为圆心所作的圆P与圆O有公共点时，试法语半径最小时，圆P的方程。
解：（1）连OP，∵Q为切点，PQ⊥OQ，由勾股定理有
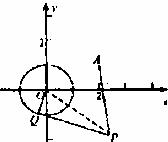
又由已知
即
化简得实数a、b间满足的等量关系为：
（2）由
故当
长的最小值为
解法2：由（1）知点P在直线
上
∴
，即求点A到直线l的距离
∴
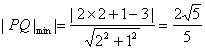
（3）设圆P的半径为R
∵圆P与圆O有公共点，圆O的半径为1，
∴
而
故当
此时
得半径取最小值时圆P的方程为
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
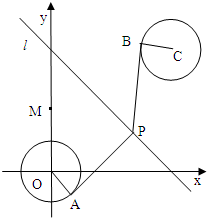已知圆O：x2+y2=1，圆C：（x-4）2+（y-4）2=1，由两圆外一点P（a，b）引两圆切线PA、PB，切点分别为A、B，如图，满足|PA|=|PB|；
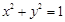和定点A(2,1)，
向圆O引切线PQ，切点为Q，且满足
．(1) 求实数a、b间满足的等量关系；
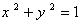和定点A（2，1），由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|， 
