题目内容

函数f（x）=alnx+x在x=1处取到极值，则a的值为

A.
$数学公式$
B.
-1
C.
0
D.
$数学公式$

B
分析：题目中条件：“函数f（x）=alnx+x在x=1处取到极值”，利用导数，
得导函数的零点是1，从而得以解决．
解答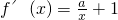：∵ $\text{[math]}$ ，
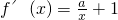∴f′（1）=0?a+1=0，
∴a=-1．
故选B．
点评：本题主要考查利用导数研究函数的极值，属于基础题．

练习册系列答案

小学升学多轮夯基总复习系列答案

金钥匙期末冲刺100分系列答案

名师指导期末冲刺卷系列答案

初中英语听力训练苏州大学出版社系列答案

教与学中考必备系列答案

培优好卷系列答案

期末在线系列答案

全程评价与自测系列答案

开心蛙口算题卡系列答案

小学升初中试卷精编系列答案

相关题目

已知x=3是函数f（x）=aln（1+x）+x²-10x的一个极值点．
（Ⅰ）求a；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）若直线y=b与函数y=f（x）的图象有3个交点，求b的取值范围．

已知函数f（x）=aln（x+1）+（x+1）²，其中，a为实常数且a≠0．
（Ⅰ）求f（x）的单调增区间；
（Ⅱ）若f(x)≥

对任意x∈（-1，+∞）恒成立，求实数a的取值范围．

已知函数f（x）=aln（1+x）-x²，当?p，q∈（0，1），且p-q＞0时，不等式f（p+1）-f（q+1）＞p-q恒成立，则实数a的取值范围为（　　）

B．[15，+∞）

D．（15，+∞）

已知函数f（x）=aln（1+e^x）-（a+1）x．
（1）已知f（x）满足下面两个条件，求a的取值范围．
①在（-∞，1]上存在极值，
②对于任意的θ∈R，c∈R直线l：xsinθ+2y+c=0都不是函数y=f（x）（x∈（-1，+∞））图象的切线；
（2）若点A（x₁，f（x₁）），B（x₂，f（x₂）），C（x₃，f（x₃））从左到右依次是函数y=f（x）图象上三点，且2x₂=x₁+x₃，当a＞0时，△ABC能否是等腰三角形？若能，求△ABC面积的最大值；若不能，请说明理由．

已知函数f（x）=aln（e^x+1）-（a+1）x，g（x）=x²-（a-1）x-f（lnx），a∈R，且g（x）在x=1处取得极值．
（1）求a的值；
（2）若对0≤x≤3，不等式g（x）≤m-8ln2成立，求m的取值范围；
（3）已知△ABC的三个顶点A，B，C都在函数f（x）的图象上，且横坐标依次成等差数列，讨论△ABC是否为钝角三角形，是否为等腰三角形．并证明你的结论．