题目内容
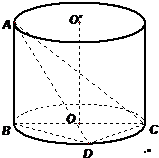如图，AB是圆柱体OO′的一条母线，BC过底面圆的圆心O，D是圆O上不与点B、C重合的任意一点，已知棱AB=5，BC=5，CD=3．（1）将四面体ABCD绕母线AB转动一周，求△ACD的三边在旋转过程中所围成的几何体的体积；
（2）二面角A-DC-B
（3）求AD与平面ABC所成的角．
分析：（1）由题意可知，所求体积是两个圆锥体的体积之差，只须分别求出这两个锥体的体积后求它们的差即得
（2）因为点D在以BC为直径的圆上，所以BD⊥DC，又可知CD⊥AD，所以∠ADB为二面角A-DC-B的平面角，在RT△ADB中，可求二面角A-DC-B的大小；
（3）过E作DE⊥BC，连接AE，因为AB⊥平面BDC，所以AB⊥DE．所以DE⊥平面ABC，所以∠DAE就是直线AD与平面ABC所成的角，故可求直线AD与平面ABC所成的角．
（2）因为点D在以BC为直径的圆上，所以BD⊥DC，又可知CD⊥AD，所以∠ADB为二面角A-DC-B的平面角，在RT△ADB中，可求二面角A-DC-B的大小；
（3）过E作DE⊥BC，连接AE，因为AB⊥平面BDC，所以AB⊥DE．所以DE⊥平面ABC，所以∠DAE就是直线AD与平面ABC所成的角，故可求直线AD与平面ABC所成的角．
解答：解：（1）由题意可知，所求体积是两个圆锥体的体积之差，
V=V圆锥ABC-V圆锥ABD=
π?52?5-
π?42?5=
-
=15π
故所求体积为15π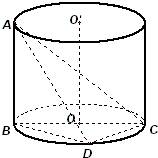
（2）因为点D在以BC为直径的圆上，所以BD⊥DC
因为AB⊥平面BDC，DC?平面BDC，所以AB⊥DC，
从而有CD⊥平面ABD，AD?平面ABD，所以CD⊥AD
所以∠ADB为二面角A-DC-B的平面角，在RT△ADB中，BD=4，
tan∠ADB=
=
，所以∠ADB=arctan
，
即二面角A-DC-B的大小为arctan
（3）过E作DE⊥BC，连接AE，因为AB⊥平面BDC，所以AB⊥DE．
所以DE⊥平面ABC
所以∠DAE就是直线AD与平面ABC所成的角；
在RT△DBC中，DE=
在RT△DBA中，AD=
在RT△ADE中，sin∠DAE=
所以，∠DAE=arcsin
所以直线AD与平面ABC所成的角为arcsin
V=V圆锥ABC-V圆锥ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 125π |
| 3 |
| 80π |
| 3 |
故所求体积为15π
（2）因为点D在以BC为直径的圆上，所以BD⊥DC
因为AB⊥平面BDC，DC?平面BDC，所以AB⊥DC，
从而有CD⊥平面ABD，AD?平面ABD，所以CD⊥AD
所以∠ADB为二面角A-DC-B的平面角，在RT△ADB中，BD=4，
tan∠ADB=
| AB |
| BD |
| 5 |
| 4 |
| 5 |
| 4 |
即二面角A-DC-B的大小为arctan
| 5 |
| 4 |
（3）过E作DE⊥BC，连接AE，因为AB⊥平面BDC，所以AB⊥DE．
所以DE⊥平面ABC
所以∠DAE就是直线AD与平面ABC所成的角；
在RT△DBC中，DE=
| 12 |
| 5 |
在RT△DBA中，AD=
| 41 |
在RT△ADE中，sin∠DAE=
12
| ||
| 205 |
所以，∠DAE=arcsin
12
| ||
| 205 |
所以直线AD与平面ABC所成的角为arcsin
12
| ||
| 205 |
点评：本题以旋转体为载体，考查几何体的条件，考查面面角，考查线面角，关键是角的寻找．
练习册系列答案
相关题目
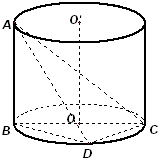如图，AB是圆柱体OO′的一条母线，BC过底面圆的圆心O，D是圆O上不与点B，C重合的任意一点，已知棱AB=5，BC=5，CD=3．
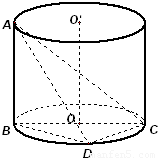如图，AB是圆柱体OO′的一条母线，BC过底面圆的圆心O，D是圆O上不与点B，C重合的任意一点，已知棱AB=5，BC=5，CD=3．
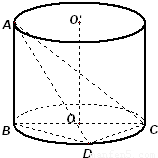如图，AB是圆柱体OO′的一条母线，BC过底面圆的圆心O，D是圆O上不与点B，C重合的任意一点，已知棱AB=5，BC=5，CD=3．