题目内容
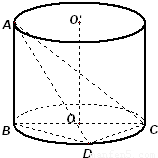 如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.
如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.(1)求直线AC与平面ABD所成的角的大小;
(2)将四面体ABCD绕母线AB转动一周,求△ACD的三边在旋转过程中所围成的几何体的体积.
【答案】分析:(1)欲求直线AC与平面ABD所成的角,先证出CD⊥平面ABD,从而得出∠CAD为直线AC与平面ABD所成的角,最后在Rt△ADC中,求解即可;
(2)由题意可知,所求体积是两个圆锥体的体积之差,只须分别求出这两个锥体的体积后求它们的差即得.
解答:解:(1)因为点D以BC径的圆上,所以BD⊥DC(2分)
因为AB⊥平面BDC,DC?平面BDC,所以AB⊥DC,
从而有CD⊥平面ABD(4分)
所以∠CAD为直线AC与平面ABD所成的角,在Rt△ADC中, =
=
,所以 ,
,
即直线AC与平面ABD所成的角为 .(6分)
.(6分)
(2)由题意可知,所求体积是两个圆锥体的体积之差,

故所求体积为15π(14分)
点评:本题主要考查了直线与平面之间所成角、棱柱、棱锥、棱台的体积,考查空间想象能力、运算能力和推理论证能力,属于中档题.
(2)由题意可知,所求体积是两个圆锥体的体积之差,只须分别求出这两个锥体的体积后求它们的差即得.
解答:解:(1)因为点D以BC径的圆上,所以BD⊥DC(2分)
因为AB⊥平面BDC,DC?平面BDC,所以AB⊥DC,
从而有CD⊥平面ABD(4分)
所以∠CAD为直线AC与平面ABD所成的角,在Rt△ADC中,
 =
=
,所以
 ,
,即直线AC与平面ABD所成的角为
 .(6分)
.(6分)(2)由题意可知,所求体积是两个圆锥体的体积之差,

故所求体积为15π(14分)
点评:本题主要考查了直线与平面之间所成角、棱柱、棱锥、棱台的体积,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
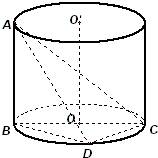 如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.
如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.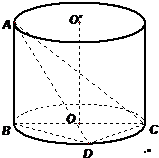 如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,已知棱AB=5,BC=5,CD=3.
如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,已知棱AB=5,BC=5,CD=3.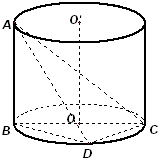 如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.
如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.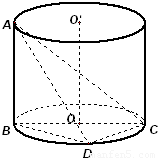 如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.
如图,AB是圆柱体OO′的一条母线,BC过底面圆的圆心O,D是圆O上不与点B,C重合的任意一点,已知棱AB=5,BC=5,CD=3.