题目内容
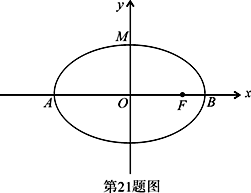
(本题15分)如图,椭圆![]() 长轴端点为
长轴端点为![]() ,
,![]()
![]() 为椭圆中心,
为椭圆中心,![]() 为椭圆的右焦点,且
为椭圆的右焦点,且![]()
![]() ,
,![]() .(1)求椭圆的标准方程;(2)记椭圆的上顶点为
.(1)求椭圆的标准方程;(2)记椭圆的上顶点为![]() ,
,![]() 直线
直线![]() 交椭圆于
交椭圆于![]() 两点,问:是否存在直线
两点,问:是否存在直线![]() ,使点
,使点![]() 恰为
恰为![]() 的垂心?若存在,求出
的垂心?若存在,求出![]() 直线
直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(1![]() )如图建系,设椭圆方程为
)如图建系,设椭圆方程为![]() ,则
,则![]()
又∵![]() 即
即 ![]()
∴![]()
故![]() 椭圆方程为
椭圆方程为![]() …………6分
…………6分
(2)假设存在直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() 恰
恰
为![]() 的垂心,则
的垂心,则![]()
![]()
设![]() ,∵
,∵![]() ,故
,故![]() , ……8分
, ……8分
于是设直线![]()
![]() 为
为 ![]() ,
,![]() 由
由![]()
![]()
 得
得![]() …10分
…10分
∵![]() 又
又![]()
得![]() 即
即
![]() 由韦达
由韦达![]() 定理
定理![]() 得
得
![]()
解得![]() 或
或![]()
![]() (舍) 经
(舍) 经![]() 检验
检验![]() 符合条件………15分
符合条件………15分

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,某小区准备绿化一块直径为
如图,某小区准备绿化一块直径为 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点。
的中点。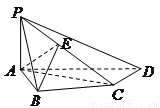
 ;
; 平面
平面 ;
; 的正切值.
的正切值.
