题目内容
如图(1)所示,直角梯形 中,
中,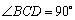 ,
,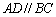 ,
, ,
,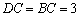 .过
.过 作
作 于
于 ,
,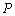 是线段
是线段 上的一个动点.将
上的一个动点.将 沿
沿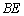 向上折起,使平面
向上折起,使平面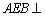 平面
平面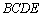 .连结
.连结 ,
, ,
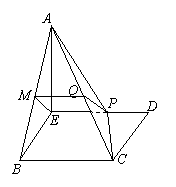
, (如图(2)).
(如图(2)).
(Ⅰ)取线段 的中点
的中点 ,问:是否存在点
,问:是否存在点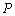 ,使得
,使得 平面
平面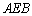 ?若存在,求出
?若存在,求出 的长;不存在,说明理由;
的长;不存在,说明理由;
 (Ⅱ)当
(Ⅱ)当 时,求平面
时,求平面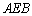 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
解:(Ⅰ)存在.当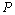 为
为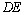 的中点时,满足
的中点时,满足 平面
平面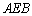 .
.
取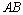 的中点
的中点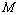 ,连结
,连结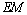 ,
,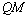 .
.
由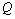 为
为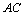 的中点,得
的中点,得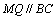 ,且
,且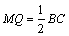 ,
,
又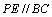 ,且
,且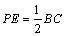 ,
,
所以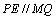 ,
,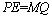 ,
,
所以四边形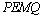 为平行四边形,
为平行四边形,
 故
故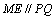 .
.
又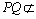 平面
平面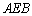 ,
,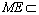 平面
平面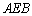 ,
,
所以 平面
平面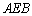 .
.
从而存在点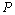 ,使得
,使得 平面
平面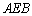 ,此时
,此时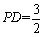 .
.
(Ⅱ)由平面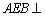 平面
平面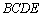 ,交线为
,交线为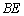 ,且
,且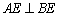 ,
,
所以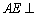 平面
平面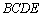 ,又
,又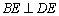 ,
,
以E为原点,分别以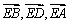 为x轴、y轴、z轴的正方向建立空间
为x轴、y轴、z轴的正方向建立空间
直角坐标系(如图),则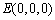 ,
,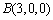 ,
,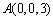 ,
,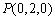 ,
,
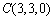 .
.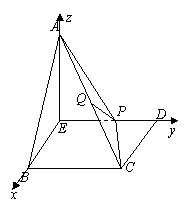
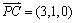 ,
,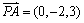 .
.
平面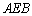 的一个法向量为
的一个法向量为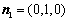 ,
,
设平面 的法向量为
的法向量为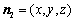 ,
,
由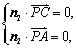 得
得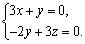
取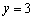 ,得
,得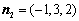 ,
,
所以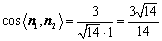 ,
,
即面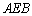 和平面
和平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为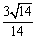

练习册系列答案
相关题目
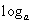 (2x2-1)的导数是( )
(2x2-1)的导数是( )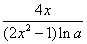 B.
B. 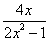 C.
C. 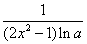 D.
D. 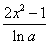
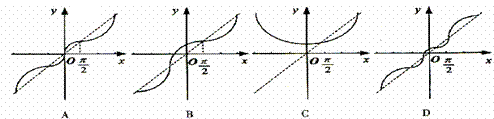 ( )
( )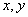 满足约束条件
满足约束条件 且
且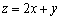 的最大值和最小值分别为
的最大值和最小值分别为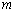 和
和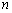 ,则
,则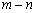 等于( )
等于( )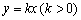 与函数
与函数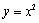 的图象交于点
的图象交于点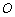 ,
, 轴于
轴于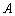 .在
.在 中任取一点,则该点落在阴影部分的概率为________.
中任取一点,则该点落在阴影部分的概率为________.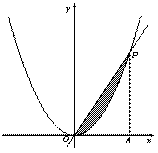

 、
、 、
、 三个平面上的正投影,则此四棱锥的体积为 ( )
三个平面上的正投影,则此四棱锥的体积为 ( )
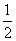 )1-x,则
)1-x,则