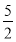题目内容
8.若实数a和b满足2×4a-2a•3b+2×9b=2a+3b+1,则2a+3b的取值范围为(1,2].分析 令2a=x>0,3b=y>0,x+y=t>0,则2×4a-2a•3b+2×9b=2a+3b+1,化为5x2-5tx+2t2-t-1=0,令f(x)=5x2-5tx+2t2-t-1,可得:f(0)=2t2-t-1>0,△=25t2-20(2t2-t-1)≥0,解出即可.
解答 解:令2a=x>0,3b=y>0,x+y=t>0,
则2×4a-2a•3b+2×9b=2a+3b+1,
化为2x2-xy+2y2=x+y+1,
即5x2-5tx+2t2-t-1=0,
令f(x)=5x2-5tx+2t2-t-1,
则f(0)=2t2-t-1>0,△=25t2-20(2t2-t-1)≥0,
解得1<t≤2,
∴2a+3b的取值范围为(1,2],
故答案为:(1,2].
点评 本题考查了指数函数的性质、二次函数与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.在平面直角坐标系中,已知点A,B在抛物线y2=4x上,且满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,点F是抛物线的焦点,设△OFA,△OFB的面积分别是S1,S2,那么S1•S2等于( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
20.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{1}{1+i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
17.在平面直角坐标系中,直线y=$\frac{\sqrt{3}}{3}$x与圆x2+y2-8x+4=0交于A、B两点,则线段AB的长为( )
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
 ,
, ,
, ,曲线
,曲线 是以点
是以点 为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在
为顶点的且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段 上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
上,问矩形的两边长分别为多少时使矩形工业园区的用地面积最大?
 ,若向量
,若向量 与
与 平行,则
平行,则 ( )
( ) B.
B.
 D.
D.