题目内容
17.在平面直角坐标系中,直线y=$\frac{\sqrt{3}}{3}$x与圆x2+y2-8x+4=0交于A、B两点,则线段AB的长为( )| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 把圆的方程化为标准形式,求出圆心和半径,再利用点到直线的距离公式求出弦心距,利用弦长公式求得线段AB的长.
解答 解:圆x2+y2-8x+4=0,即圆(x-4)2+y2 =12,圆心(4,0)、半径等于2$\sqrt{3}$.
由于弦心距d=$\frac{|\frac{\sqrt{3}}{3}×4-0|}{\sqrt{\frac{1}{3}+1}}$=2,∴弦长为2$\sqrt{{r}^{2}{-d}^{2}}$=4$\sqrt{2}$,
故选:A.
点评 本题主要考查求圆的标准方程的方法,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
5.已知点A是半径为1的⊙O外一点,且AO=2,若M,N是⊙O一条直径的两个端点,则$\overrightarrow{AM}$$•\overrightarrow{AN}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.已知集合M={1,4,7},M∪N=M,则集合N不可能是( )
| A. | ∅ | B. | {1,4} | C. | M | D. | {2,7} |
 为
为 内一点,满足
内一点,满足 ,且
,且 ,则
,则 的面积为____________.
的面积为____________.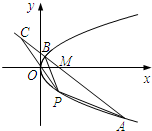 如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.
如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.