题目内容
(本小题满分12分)已知函数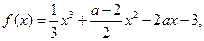
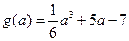 ,
,
(1)当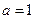 时,求函数
时,求函数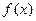 的单调递增区间;
的单调递增区间;
(2)若函数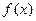 在[
在[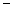 2,0]上不单调,且
2,0]上不单调,且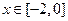 时,不等式
时,不等式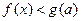 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
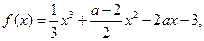
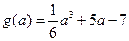 ,
,(1)当
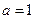 时,求函数
时,求函数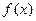 的单调递增区间;
的单调递增区间;(2)若函数
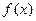 在[
在[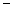 2,0]上不单调,且
2,0]上不单调,且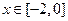 时,不等式
时,不等式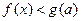 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.(1)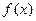 单调递增区间是:
单调递增区间是:
(2)a的取值范围是(1,2)
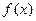 单调递增区间是:
单调递增区间是:
(2)a的取值范围是(1,2)
(1)当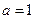 时,
时, 定义域为R,
定义域为R,
 ……………………………………………………………………2分
……………………………………………………………………2分
令 ……………………………………………………4分
……………………………………………………4分
∴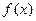 单调递增区间是:
单调递增区间是: ……………………………………5分
……………………………………5分
(2)∵
令 得
得
∵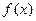 在区间
在区间 上不单调
上不单调
∴ ……………………………………………………6分
……………………………………………………6分
又∵在 上,
上, ,在
,在 上
上
∴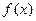 在
在 上有唯一的极大值点
上有唯一的极大值点
∴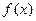 在
在 上的最大值为
上的最大值为 …………………………………………8分∴当
…………………………………………8分∴当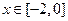 时,不等式
时,不等式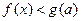 恒成立,等价于
恒成立,等价于
∴
即 …………………………………………………11分
…………………………………………………11分
综上a的取值范围是(1,2) 12分
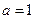 时,
时, 定义域为R,
定义域为R,
 ……………………………………………………………………2分
……………………………………………………………………2分令
 ……………………………………………………4分
……………………………………………………4分∴
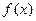 单调递增区间是:
单调递增区间是: ……………………………………5分
……………………………………5分(2)∵

令
 得
得
∵
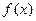 在区间
在区间 上不单调
上不单调∴
 ……………………………………………………6分
……………………………………………………6分又∵在
 上,
上, ,在
,在 上
上
∴
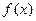 在
在 上有唯一的极大值点
上有唯一的极大值点
∴
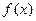 在
在 上的最大值为
上的最大值为 …………………………………………8分∴当
…………………………………………8分∴当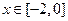 时,不等式
时,不等式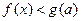 恒成立,等价于
恒成立,等价于
∴

即
 …………………………………………………11分
…………………………………………………11分综上a的取值范围是(1,2) 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
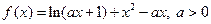 ,
,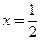 是函数
是函数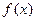 的一个极值点,求
的一个极值点,求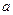 ;
;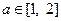 ,不等式
,不等式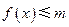 在
在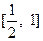 上恒成立,求
上恒成立,求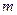 的取值范围.
的取值范围.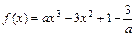 .(a>0)
.(a>0)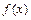 的单调性;
的单调性;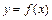 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.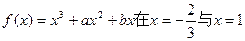 处都取得极值.
处都取得极值.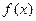 的单调区间及极大值、极小值
的单调区间及极大值、极小值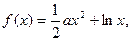
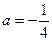 时,求
时,求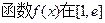 上的最大值、最小值:
上的最大值、最小值: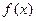 的单调区间;
的单调区间;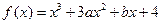 在
在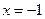 时有极值0,则常数
时有极值0,则常数 .
.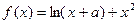
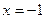 时,
时,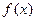 取得极值,求
取得极值,求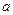 值,并讨论
值,并讨论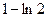
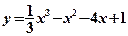 ,直线
,直线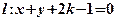 ,当
,当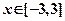 时,直线
时,直线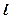 恒在曲线C的上方,则实数
恒在曲线C的上方,则实数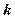 的取值范围是 ( )
的取值范围是 ( )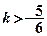
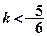
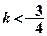
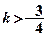
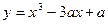 在(1,2)内有极小值,则实数a的取值范围是( )
在(1,2)内有极小值,则实数a的取值范围是( )


