Question

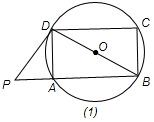已知：四边形ABCD为圆内接矩形，过点D作圆的切线DP，交BA的延长线于点P，且PD=15，PA=9．求AD与AB的长．

Answer 1

分析：由四边形是圆内接矩形可知，∠PAD=90°．根据勾股定理便可求出AD的长，因为PD是⊙O的切线，所以根据切线的性质和直径所对的圆周角是90°构造直角三角形，应用三角函数即可求出AD与AB的长；

解答：解：连接BD．（如图1）
∵四边形ABCD是矩形，
∴AD⊥PB．
∴∠PAD=∠BAD=90°．△PAD与△ABD都是直角三角形．
∵PD=15，PA=9，
∴AD=12．
∵DP切⊙O于D，
∴BD⊥DP．
∴∠PDB=90°．
∵∠P+∠ADP=∠ADP+∠ADB=90°，
∴∠P=∠ADB．
∵tan∠P=

AD

AP

=

12

9

=

4

3

，
∴tan∠ADB=

AB

AD

=

4

3

．
∴AB=AD•tan∠ADB=

12×4

3

=16．

点评：此题不仅考查了求圆的弦长等基础知识，还考查了圆的切线的性质定理的证明．