题目内容
已知正项等比数列{an}满足：a7=a6+2a5若存在两项am、an使得
，则
的最小值为 ．
【答案】分析：由已知中正项等比数列{an}满足：a7=a6+2a5，我们易求出数列的公比，再结合存在两项am、an使得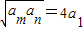
，我们可以求出正整数m，n的和，再结合基本不等式中“1”的活用，即可得到答案．
解答：解：设等比数列{an}的首项为a1，公比为q，
∵a7=a6+2a5，则a1•q6=a1•q5+2a1•q4
即q2-q-2=0，解得q=2或q=-1（舍去）
若
，
则m+n=6
则6（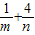
）=（m+n）（
）=5+（
）≥5+4=9
则
故答案为
点评：本题考查的知识点是等比数列的性质，基本不等式，其中根据已知中正项等比数列{an}满足：a7=a6+2a5若存在两项am、an使得
，将问题转化为用基本不等式求最值是解答本题的关键．
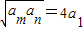，我们可以求出正整数m，n的和，再结合基本不等式中“1”的活用，即可得到答案．解答：解：设等比数列{an}的首项为a1，公比为q，
∵a7=a6+2a5，则a1•q6=a1•q5+2a1•q4
即q2-q-2=0，解得q=2或q=-1（舍去）
若
，则m+n=6
则6（
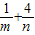）=（m+n）（）=5+（）≥5+4=9则
故答案为
点评：本题考查的知识点是等比数列的性质，基本不等式，其中根据已知中正项等比数列{an}满足：a7=a6+2a5若存在两项am、an使得
，将问题转化为用基本不等式求最值是解答本题的关键． 
练习册系列答案
相关题目
已知正项等比数列{an}中，a1=1，a3a7=4a62，则S6=（ ）
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知正项等比数列{an}满足：a7=a6+2a5，若存在两项am，an使得
=4a1，则
+
的最小值为（ ）
| aman |
| 1 |
| m |
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
已知正项等比数列{an}的前n项和为Sn，若S3=3，S9-S6=12，则S6=（ ）
| A、9 | ||
B、
| ||
| C、18 | ||
| D、39 |