题目内容
若直线y=x+t被圆x2+y2=8截得弦长大于等于
,则t的取值范围为( )
4
| ||
| 3 |
分析:根据弦长的关系确定圆心与直线的距离关系即可求解t的取值范围.
解答:解:由圆x2+y2=8可知圆心为O(0,0),半径r=
=2
.
设直线截得弦长为l,圆心到直线的距离为d,
则l≥
,在圆中d2=r2-(
)2=8-
,
∵l≥
,∴l2≥
,
≥
,
∴d2=8-
≤8-
=
,即d≤
=
.
由点到直线的距离公式得圆心O到直线y=x+t即x-y+t=0的距离为d=
≤
,
∴|t|≤
,即-
≤t≤
.
故t的取值范围为[-
,
].
故选:D.
| 8 |
| 2 |
设直线截得弦长为l,圆心到直线的距离为d,
则l≥
4
| ||
| 3 |
| l |
| 2 |
| l2 |
| 4 |
∵l≥
4
| ||
| 3 |
| 32 |
| 9 |
| l2 |
| 4 |
| 8 |
| 9 |
∴d2=8-
| l2 |
| 4 |
| 8 |
| 9 |
| 64 |
| 9 |
|
| 8 |
| 3 |
由点到直线的距离公式得圆心O到直线y=x+t即x-y+t=0的距离为d=
| |t| | ||
|
| 8 |
| 3 |
∴|t|≤
8
| ||
| 3 |
8
| ||
| 3 |
8
| ||
| 3 |
故t的取值范围为[-
8
| ||
| 3 |
8
| ||
| 3 |
故选:D.
点评:本题主要考查直线与圆的位置关系的应用,以及点到直线的距离公式,考查学生的运算能力.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
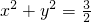 ,直线l被圆截得的弦长与椭圆C:
,直线l被圆截得的弦长与椭圆C: 的短轴长相等,椭圆的离心率
的短轴长相等,椭圆的离心率 .
. )的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.