题目内容
如图,三棱柱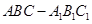 的所有棱长都为
的所有棱长都为 ,且
,且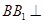 平面
平面 ,
, 为
为 中点.
中点.
(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求二面角 的大小的余弦值;
的大小的余弦值;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
(1)欲证AB1⊥平面A1BD,根据直线与平面垂直的判定定理可知只需证AB1与平面A1BD内两相交直线垂直,而AB1⊥A1B,AB1⊥DO,A1B∩DO=O,满足定理所需条件.
(2)
(3)
解析试题分析:解析: (Ⅰ)取 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, .
. 平面
平面 ,
, 平面
平面
 平面
平面 平面
平面 ,
, 平面
平面 . 1分
. 1分
取 中点
中点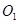 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
,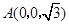 ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
, .
. 平面
平面 . 4分
. 4分
(Ⅱ)设平面 的法向量为
的法向量为 .
. ,
, .
. ,
, ,
,

取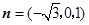 为平面
为平面 的一个法向量.
的一个法向量.
由(Ⅰ)知 平面
平面 ,
, 为平面
为平面 的法向量.
的法向量. ,
, .
. 二面角
二面角 的余弦值为
的余弦值为 . 9分
. 9分
(Ⅲ)由(Ⅱ),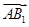 为平面
为平面 法向量,
法向量, .
. 点
点 到平面
到平面 的距离
的距离 . 13分
. 13分
考点:空间中角和距离的求解
点评:主要是考查了运用向量法来求解空间中的角和距离的求解,属于中档题。

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 的棱长为1,点
的棱长为1,点 分别是
分别是 和
和 的中点
的中点

 与
与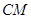 所成角的余弦值。
所成角的余弦值。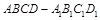 ,中,
,中, ,点
,点 在棱AB上移动.
在棱AB上移动.
 ;
;  的中点时,求点
的中点时,求点 的距离;
的距离;  等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
. ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G

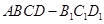 中,四边形
中,四边形 为菱形,
为菱形, ,
, ,面
,面 ∥面
∥面 、
、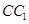 、
、 都垂直于面
都垂直于面 ,
, 为
为
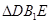 为等腰直角三角形;
为等腰直角三角形; ∥面
∥面 .
.
 平面ADE;
平面ADE; 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,AC、BD交于点G.
,AC、BD交于点G.
 ;
; ;
; 的体积.
的体积. 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, 的中点,M是线段
的中点,M是线段 上的动点。
上的动点。
 ,请给出证明;
,请给出证明;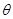 ,求
,求 的最大值。
的最大值。