题目内容
已知数列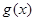 的前n项和为
的前n项和为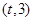 ,
,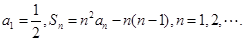
(1)证明:数列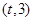 是等差数列,并求
是等差数列,并求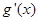 ;
;
(2)设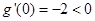 ,求证:
,求证: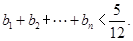
(1)证明略, ,(2)详见解析.
,(2)详见解析.
解析试题分析:(1)利用 代入
代入 得关于
得关于 的递推公式,然后变形为
的递推公式,然后变形为 ,利用等差数列的定义即可说明;
,利用等差数列的定义即可说明;
(2)由已知可得 ,利用裂项求和法求
,利用裂项求和法求 ,然后放缩一下即可.
,然后放缩一下即可.
试题解析:(1)证明:由 知,当
知,当 时:
时: ,
,
即 ,∴
,∴ ,对
,对 成立.
成立.
又 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列. ,∴
,∴ . 6分
. 6分
(2) , 8分
, 8分
∴
= . 12分
. 12分
考点:(1)等差数列的定义;(2)裂项求和法.

练习册系列答案
相关题目
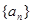 是等差数列,
是等差数列,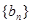 是等比数列,其中
是等比数列,其中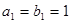 ,
,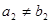 ,且
,且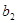 为
为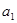 、
、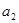 的等差中项,
的等差中项,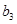 的等差中项.
的等差中项.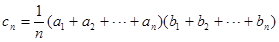 ,求数列
,求数列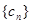 的前
的前 项和
项和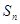 .
.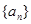 是正数组成的数列,其前
是正数组成的数列,其前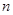 项和为
项和为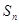 ,且对所有的正整数
,且对所有的正整数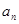 与2的等差中项等于
与2的等差中项等于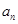 }的前n项和为S,且S3=2S2+4,a5=36.
}的前n项和为S,且S3=2S2+4,a5=36.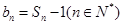 ,
,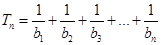 ,求Tn
,求Tn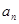 }中,
}中,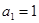 ,
,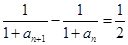
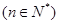 ,
,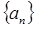 的通项公式
的通项公式 (
(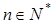 ),求数列
),求数列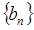 的前10项和
的前10项和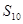 .
.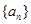 的各项均为正数,其前
的各项均为正数,其前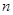 项和为
项和为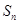 ,且
,且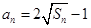 ,
,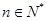 ,数列
,数列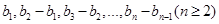 是首项和公比均为
是首项和公比均为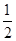 的等比数列.
的等比数列.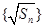 是等差数列;
是等差数列;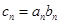 ,求数列
,求数列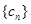 的前
的前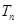 .
.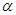 为锐角,且
为锐角,且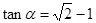 ,函数
,函数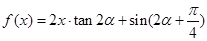 ,数列
,数列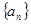 的首项
的首项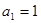 ,
, .
.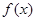 的表达式;(2)求数列
的表达式;(2)求数列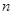 项和
项和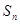 .
.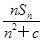 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.