题目内容
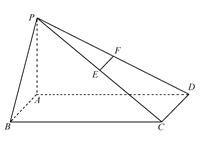
(12分)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,

(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积.

(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积.
(Ⅰ)证:设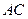 与
与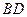 交于点
交于点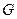 ,则
,则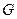 为
为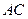 的中点,连
的中点,连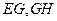 ,由于
,由于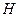 为
为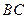 的中点,故
的中点,故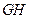
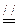
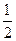
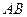 ,又
,又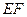
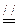
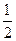
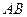 ,
,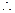 四边形
四边形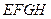 为平行四边形,
为平行四边形, 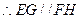 ,而
,而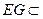 平面
平面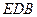 ,
,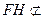 平面
平面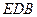 ,
,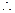
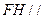 平面
平面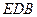 (4分)
(4分)
(Ⅱ)证:由四边形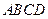 为正方形,
为正方形,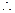
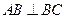
又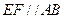 ,
,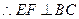 .而
.而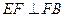 ,
,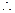
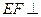 平面
平面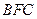 ,
,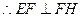
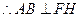 ,
,
又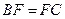 ,
,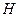 为
为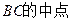 ,
,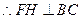 ,且
,且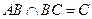
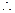
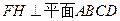
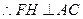 ,又
,又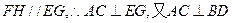 ,
,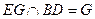
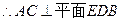 (8分)
(8分)
(Ⅲ)解: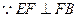 ,
,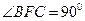 ,
,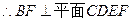
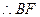 为四面体
为四面体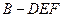 的高,又
的高,又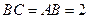 ,
,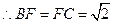
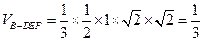 (12分)
(12分)
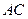 与
与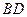 交于点
交于点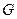 ,则
,则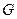 为
为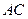 的中点,连
的中点,连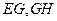 ,由于
,由于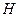 为
为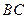 的中点,故
的中点,故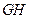
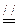
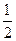
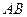 ,又
,又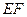
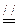
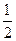
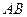 ,
, 四边形
四边形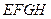 为平行四边形,
为平行四边形, 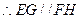 ,而
,而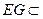 平面
平面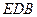 ,
,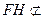 平面
平面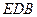 ,
,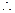
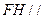 平面
平面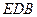 (4分)
(4分)(Ⅱ)证:由四边形
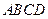 为正方形,
为正方形,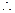
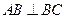
又
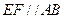 ,
,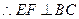 .而
.而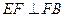 ,
,
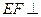 平面
平面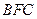 ,
,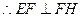
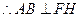 ,
,又
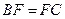 ,
,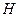 为
为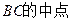 ,
,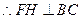 ,且
,且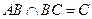
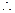
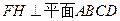
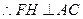 ,又
,又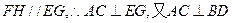 ,
,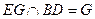
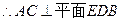 (8分)
(8分)(Ⅲ)解:
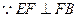 ,
,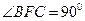 ,
,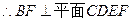
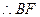 为四面体
为四面体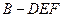 的高,又
的高,又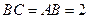 ,
,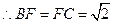
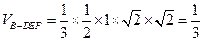 (12分)
(12分)略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
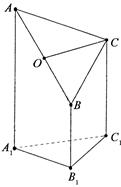
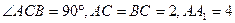 。E、F分别是棱CC1、AB中点。
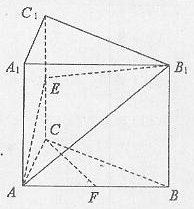
。E、F分别是棱CC1、AB中点。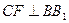 ;
;
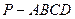 中,
中,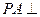 底面
底面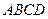 ,
,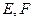 分
分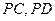 的中点,求证:
的中点,求证: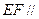 平面
平面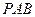 ;
;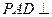 平面
平面 .
.
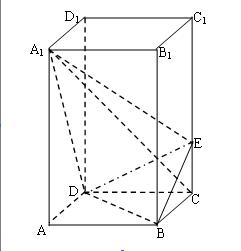
 中,
中,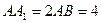 ,点
,点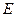 在
在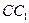 上且
上且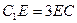 .
.
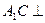 平面
平面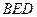 ;
;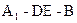 的余弦值.
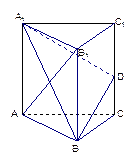
的余弦值.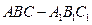 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由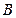 沿棱柱侧面经过棱
沿棱柱侧面经过棱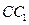 到点
到点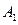 的最短路线长为
的最短路线长为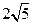 ,设这条最短路线与
,设这条最短路线与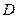 .
.
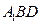 内是否存在过
内是否存在过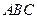 平行?证明你的判断;
平行?证明你的判断;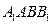 .
.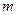 、
、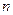 ,平面
,平面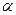 、
、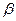 ,给出下列命题:
,给出下列命题:
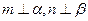 ,且
,且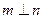 ,则
,则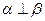 ②若
②若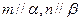 ,且
,且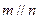 ,则
,则
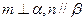 ,且
,且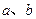 ,高为
,高为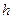 ,且侧面积等于两底面积之和,则下列关系正确的是
,且侧面积等于两底面积之和,则下列关系正确的是