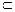题目内容
(本小题满分12分)
右图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到
的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,
AAl=4,BBl=2,CCl=3.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求二面角B—AC—A1的大小;
(3)求此几何体的体积.
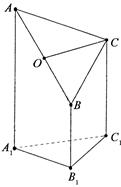
右图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到
的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,
AAl=4,BBl=2,CCl=3.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求二面角B—AC—A1的大小;
(3)求此几何体的体积.

(1)OC∥平面A1B1C1
(2) 二面角的大小为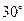
(3)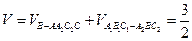
(2) 二面角的大小为
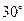
(3)
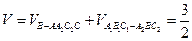
(1)证明:作 交
交 于
于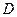 ,连
,连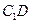 .
.
 则
则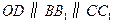 .
.
因为 是
是 的中点,
的中点,
所以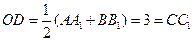 .
.
则 是平行四边形,因此有
是平行四边形,因此有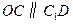 .
.
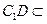 平面
平面 且
且 平面
平面 ,
,
则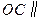 面
面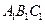 .
.
(2)如图,过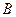 作截面
作截面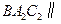 面
面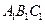 ,分别交
,分别交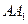 ,
, 于
于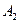 ,
,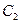 .
.
作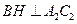 于
于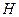 ,连
,连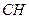 .
.
因为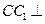 面
面 ,所以
,所以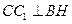 ,则
,则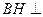 平面
平面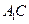 .
.
又因为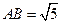 ,
,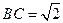 ,
,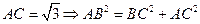 .
.
所以 ,根据三垂线定理知
,根据三垂线定理知 ,所以
,所以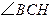 就是所求二面角的平面角.
就是所求二面角的平面角.
因为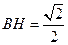 ,所以
,所以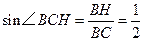 ,故
,故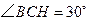 ,
,
即:所求二面角的大小为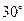 .
.
(3)因为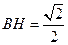 ,所以
,所以
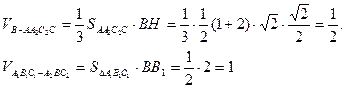
所求几何体体积为
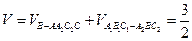 .
.
解法二:
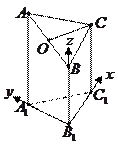 (1)如图,以
(1)如图,以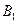 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
则 ,
,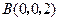 ,
,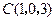 ,因为
,因为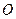 是
是 的中点,所以
的中点,所以 ,
,
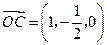 .
.
易知,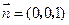 是平面
是平面 的一个法向量.
的一个法向量.
因为 ,
, 平面
平面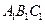 ,所以
,所以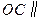 平面
平面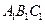 .
.
(2)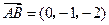 ,
,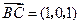 ,
,
设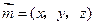 是平面
是平面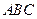 的一个法向量,则
的一个法向量,则
则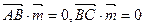 得:
得:
取 ,
,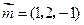 .
.
显然,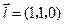 为平面
为平面 的一个法向量.
的一个法向量.
则 ,
,
结合图形可知所求二面角为锐角.
所以二面角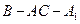 的大小是
的大小是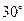 .
.
(3)同解法一.
 交
交 于
于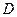 ,连
,连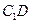 .
. 则
则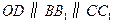 .
.因为
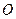 是
是 的中点,
的中点,所以
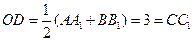 .
.则
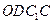 是平行四边形,因此有
是平行四边形,因此有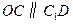 .
.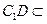 平面
平面 且
且 平面
平面 ,
,则
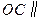 面
面 .
.(2)如图,过
 作截面
作截面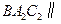 面
面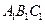 ,分别交
,分别交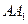 ,
, 于
于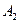 ,
,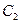 .
.作
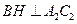 于
于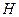 ,连
,连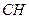 .
.因为
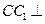 面
面 ,所以
,所以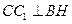 ,则
,则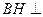 平面
平面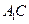 .
.又因为
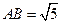 ,
,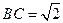 ,
,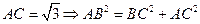 .
.所以
 ,根据三垂线定理知
,根据三垂线定理知 ,所以
,所以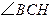 就是所求二面角的平面角.
就是所求二面角的平面角.因为
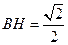 ,所以
,所以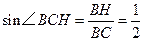 ,故
,故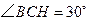 ,
,即:所求二面角的大小为
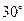 .
.(3)因为
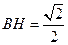 ,所以
,所以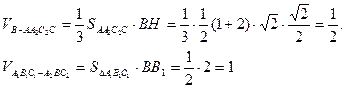
所求几何体体积为
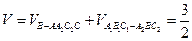 .
.解法二:
 (1)如图,以
(1)如图,以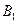 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,则
 ,
,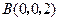 ,
,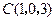 ,因为
,因为 是
是 的中点,所以
的中点,所以 ,
,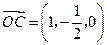 .
.易知,
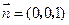 是平面
是平面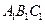 的一个法向量.
的一个法向量.因为
 ,
, 平面
平面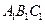 ,所以
,所以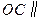 平面
平面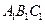 .
.(2)
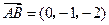 ,
,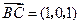 ,
,设
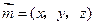 是平面
是平面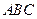 的一个法向量,则
的一个法向量,则则
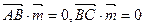 得:
得:
取
 ,
,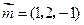 .
.显然,
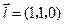 为平面
为平面 的一个法向量.
的一个法向量.则
 ,
,结合图形可知所求二面角为锐角.
所以二面角
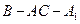 的大小是
的大小是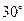 .
.(3)同解法一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

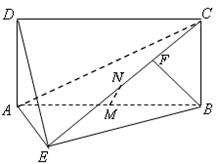
 中,
中,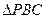 为正三角形,
为正三角形, ,
, 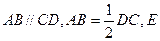 为
为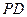 中点
中点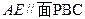 ;(2)求证:
;(2)求证:
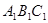 中,
中,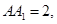 AB = 1,
AB = 1,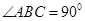 ;点D、E分别在
;点D、E分别在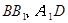 上,且
上,且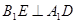 ,四棱锥
,四棱锥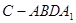 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。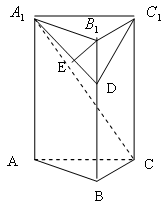
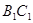 的距离;(8分)
的距离;(8分)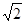 ,求二面角
,求二面角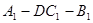 的平面角的正切值。(5分)
的平面角的正切值。(5分)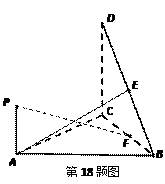
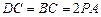 ,
,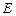 为DB的中点,
为DB的中点,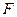 是线段
是线段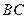 上的动点,设平面
上的动点,设平面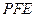 与平面
与平面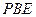 所成的平面角大小为
所成的平面角大小为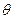 ,当
,当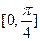 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。 (1) 求证:BD1∥平面C1DE;
(1) 求证:BD1∥平面C1DE;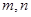 是不同的直线,
是不同的直线,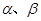 是不重合的平面,下列命题为真命题的是( )
是不重合的平面,下列命题为真命题的是( )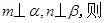
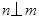
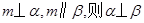
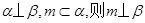

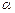 、
、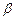 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )