题目内容
1.已知函数f(x)=lnx+mx2(m∈R).(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若m=0,A(a,f(a))、B(b,f(b))是函数f(x)图象上不同的两点,且a>b>0,f′(x)为f(x)的导函数,求证:f′($\frac{a+b}{2}$)<$\frac{f(a)-f(b)}{a-b}$<f′(b);
(Ⅲ)求证:$\frac{2}{3}+\frac{2}{5}+\frac{2}{7}+…+\frac{2}{2n+1}$<ln(n+1)<1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$(n∈N*).
分析 (Ⅰ)通过函数f(x)的解析式可知其定义域为(0,+∞)、f′(x)=$\frac{1+2m{x}^{2}}{x}$,结合导数知识分m≥0、m<0两种情况讨论即可;
(Ⅱ)通过(I)及m=0可知问题转化为证明$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$.对于要证$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$,通过换元法即证函数g(t)=lnt-t+1满足g(t)<g(1)=0即可;对于要证$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$,通过换元法令t=$\frac{a}{b}$,即证(t+1)lnt-2(t-1)>0,通过令h(t)=(t+1)lnt-2t+2,利用h″(t)>0可知h′(t)>h′(1)=0,从而可得结论;
(Ⅲ)通过(II)可知$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$(a>b>0),通过令a=n+1、b=n可知$\frac{2}{2n+1}$<ln(n+1)-lnn<$\frac{1}{n}$,利用ln(n+1)=[ln(n+1)-lnn]+…+(ln3-ln2)+(ln2-ln1)累加计算即得结论.
解答 (Ⅰ)解:依题意,f(x)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$+2mx=$\frac{1+2m{x}^{2}}{x}$,
当m≥0时,f(x)在(0,+∞)上单调递增;
当m<0时,令f′(x)=0得x=$\sqrt{-\frac{1}{2m}}$,
当x∈(0,$\sqrt{-\frac{1}{2m}}$)时f′(x)>0,此时f(x)在区间(0,$\sqrt{-\frac{1}{2m}}$)上单调递增;
当x∈($\sqrt{-\frac{1}{2m}}$,+∞)时f′(x)<0,此时f(x)在区间($\sqrt{-\frac{1}{2m}}$,+∞)上单调递减;
综上所述,当m≥0时f(x)在(0,+∞)上单调递增;当m<0时f(x)在(0,$\sqrt{-\frac{1}{2m}}$)上单调递增、在($\sqrt{-\frac{1}{2m}}$,+∞)上单调递减;
(Ⅱ)证明:由(I)及m=0可知f(x)=lnx、f′(x)=$\frac{1}{x}$,
∴要证f′($\frac{a+b}{2}$)<$\frac{f(a)-f(b)}{a-b}$<f′(b),即证$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$.
要证$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$,只需证ln$\frac{a}{b}$<$\frac{a}{b}$-1,
令t=$\frac{a}{b}$,则t>1,即证lnt-t+1<0,
令g(t)=lnt-t+1,则g′(t)=$\frac{1}{t}$-1<0,
∴g(t)<g(1)=0,得证;
要证$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$,只需证ln$\frac{a}{b}$>$\frac{2(\frac{a}{b}-1)}{\frac{a}{b}+1}$,
令t=$\frac{a}{b}$,则t>1,即证(t+1)lnt-2(t-1)>0,
令h(t)=(t+1)lnt-2t+2,则h′(t)=lnt+$\frac{1}{t}$-1,
∵h″(t)=$\frac{1}{t}$-$\frac{1}{{t}^{2}}$=$\frac{1}{t}$(1-$\frac{1}{t}$)>0,
∴h′(t)>h′(1)=0,
∴h(t)>h(1)=0,得证;
综上所述,f′($\frac{a+b}{2}$)<$\frac{f(a)-f(b)}{a-b}$<f′(b);
(Ⅲ)证明:由(II)可知$\frac{2}{a+b}$<$\frac{lna-lnb}{a-b}$<$\frac{1}{b}$(a>b>0),
令a=n+1、b=n,则有$\frac{2}{2n+1}$<ln(n+1)-lnn<$\frac{1}{n}$,
∵ln(n+1)=[ln(n+1)-lnn]+…+(ln3-ln2)+(ln2-ln1),
∴$\frac{2}{3}+\frac{2}{5}+\frac{2}{7}+…+\frac{2}{2n+1}$<ln(n+1)<1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$(n∈N*).
点评 本题是一道关于函数与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于难题.

 如图,两曲线y=3-x2与y=x2-2x-1所围成的图形面积是( )
如图,两曲线y=3-x2与y=x2-2x-1所围成的图形面积是( )| A. | 6 | B. | 9 | C. | 12 | D. | 3 |
| A. | [12,24] | B. | [8,12] | C. | [8,24] | D. | [8,17] |
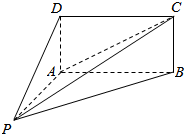 已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.